Сначала раскрываешь скобки потом переносишь числа с не известным в право а обычные в право дальше решаешь.
a) 3.8x - (1.6 - 1.2x) = 9.6 + (3.7 - 5x)
3.8x - 1.6 + 1.2x = 9.6 + 3.7 - 5x
3.8x + 1.2x + 5x = 9.6 + 3.7 + 1.6
10x = 14.9
x = 1.49
b) (4.5y + 9) - (6.2 - 3.1y) = 7.2y + 2.8
4.5y + 9 - 6.2 + 3.1y = 7.2y + 2.8
4.5y + 3.1y - 7.2y = 2.8 - 9 + 6.2
0.4y = 0
y = 0
c) 0.6m - 1.4 = (3.5m + 1.7) - (2.7m - 3.4)
0.6m - 1.4 = 3.5m + 1.7 - 2.7m + 3.4
0.6m - 3.5m + 2.7m = 1.7 + 3.4 + 1.4
-0.2m = 6.5
m = -32.5
d) (5.3a - 0.8) - (1.6 - 4.7a) = 2a - (a - 0.3)
5.3a - 0.8 - 1.6 + 4.7a = 2a - a + 0.3
5.3a + 4.7a - 2a + a = 0.3 + 0.8 + 1.6
9a = 2.7
a = 0.3
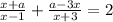
ОДЗ: 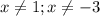
Перенесем 2 в левую часть и преобразуем:
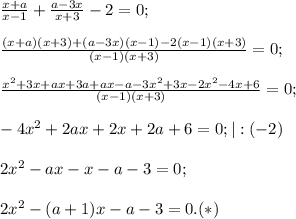
Ищем дискриминант, так как уравнение априори квадратное:
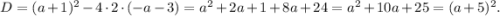
Исходное уравнение имеет единственное решение в двух случаях.
1) уравнение (*) имеет одно решение (D=0), которое удовлетворяет ОДЗ. Дискриминант равен 0 при a = -5. Тогда корень уравнения равен 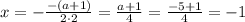 . Он удовлетворяет ОДЗ, поэтому a = -5 точно пойдет в ответ.
. Он удовлетворяет ОДЗ, поэтому a = -5 точно пойдет в ответ.
2) уравнение (*) имеет два решения(D>0), но один из корней отпадает по ОДЗ.
Дискриминант положителен при a ≠ -5. Тогда корни уравнения равны
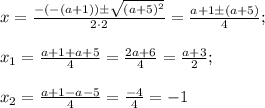
Один из корней - x = -1 - удовлетворяет ОДЗ при любом значении параметра, поэтому корень x = (a+3)/2 должен наоборот не удовлетворять, чтобы решение было ровно одно.
Проверим, при каких a корень x = (a+3)/2 совпадает с числами 1 или -3:
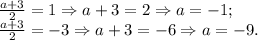
Итого нам подходят только три значения a: a = -9, a =-5, a = -1.
ОТВЕТ: a ∈ {-9; -5; -1}