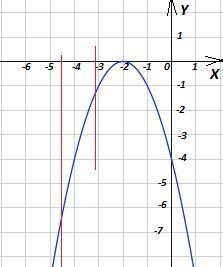
y = -x² - 4x - 4 = -(x + 2)² - квадратичная функция, график - парабола, ветви направлены вниз (-1 < 0). Вершина параболы в точке (-2;0) - из уравнения параболы.
A) x ≤ -2; Так как вершина параболы в точке (-2; 0) и ветви направлены вниз, значит, на интервале x∈(-∞; -2] функция монотонно возрастает.
Б) Максимум функции в точке (-2; 0). Абсцисса вершины не принадлежит заданному интервалу : x₀ = -2 ∉ [-4,5; -3,1]
Значения функции на границах интервала
y(-4,5) = -(-4,5 + 2)² = -(-2,5)² = -6,25 - наименьшее значение
y(-3,1) = -(-3,1 + 2)² = -(-1,1)² = -1,21 - наибольшее значение
3x + 2y = 5
2x^2 - y^2 = 14
2y = 5-3x
2x^2 - y^2 = 14
y = 5-3x/2
2x^2 - (5-3x/2)^2= 14
y = 5-3x/2
2x^2 - 25-30x+x^2/4= 14
y = 5-3x/2
8x^2 - 25-30x+x^2/4= 14
y = 5-3x/2
9x^2-30x-25=14*4
y=5-3x/2
9x^2-30x-25=56
y=5-3x/2
9x^2-30x-81=0
y=5-3x/2
3x^2-10x-27=0. discrimenant=25+81=106
y=5-3x/2. x1=5-10kornei iz 6/3
x2=5+10kornei iz 6/3
x1= 5-10kornei iz 6/3
y=5-15+30kornei iz 6/3= 30kornei iz 6/3-10
ili
x2=5+ 10kornei iz 6/3
y=5-15-30kornei iz 6/3=-10- 30kornei iz 6/3