Из 40 + 60 = 100 г. раствора соль составляет
(40 * 20 + 60 * 30) / 100 = 2600 / 100 = 26 г, поэтому концентрация раствора
26 / 100 * 100% = 26%
а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
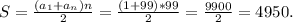
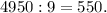
Так как получилось разделить нацело, то 1234...9899 делится на 9.
ответ:1) Задание
Дана функция
найти промежутки возрастания и убывания
По признаку возрастания и убывания функции на интервале:
если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Найдем производную данной функции
найдем точки экстремума, точки в которых производная равна нулю
отметим точки на числовой прямой и проверим знак производной на промежутках
___+-+__
0 2
Значит на промежутках (-оо;0) ∪ (2;+оо) функция возрастает
на промежутке (0;2) функция убывает
точки х=0 точка минимума, х=2 точка максимума
Найти наибольшее и наименьшее значение функции на отрезке [-2; 1].
Заметим, что х=2 точка максимума не входит в данный промежуток,
а х=0 принадлежит данному промежутку
Проверим значение функции в точке х=0 и на концах отрезка
Значит наибольшее значение функции на отрезке [-2;1]
в точке х=0 и у(0)=1
значит наименьшее значение функции на отрезке [-2;1]
в точке х=-2 и у(-2)= -19
2. Напишите уравнение к касательной к графику функции
f(x)=x^3-3x^2+2x+4 в точке с абсциссой x0=1.
Уравнение касательной имеет вид
найдем производную данной функции
найдем значение функции и производной в точке х=1
подставим значения в уравнение касательной
Объяснение:
Смешали 40г 20% -го и 60г 30% растворов соли. получили 100г х% раствора
0,2*40 + 0,3*60=100х
8+18=100х
26=100х
х=0,26
получили раствор 100г 26%-ого соляного р-ра