При каких значениях a многочлен f(x)=2x^4+ax^3-9x^2+23x-20 можно разделить на многочлен g(x)=x^2+3x-a ? желательно при решении воспользоваться теоремой безу. ^-это степень.
Согласно теореме Безу остаток от деления полинома на двучлен равен значению полинома в корне этого двучлена,в данной задаче на полином G(x) никаких дополнительных условий не наложено,значит он может быть неприводимым над полем вещественных чисел,однако все равно раскладываться в произведение двучленов вида
Где комплексно сопряжен z.
Полином G(x) примет вид
Re(z)-вещественная часть z,-модуль числа z.
Очевидно,что подставляя получившиеся корни в исходный многочлен используя теорему Безу вычисление получается мягко говоря неудобным.
Аналогичная ситуация со схемой Горнера.
А вот при делении полиномов столбиком исходный многочлен представим в виде:
Очевидно,что степень остатка должна быть меньше степени делителя и мы можем остаток разделить на полином G(x),домноженный на (-a-3),тогда для того чтобы остаток от деления был равен нулю,то есть чтобы F(x) делился на G(x) должна выполняться система:
Которая не имеет решений ни в поле действительных,ни в поле комплексных чисел.
Значит ни при каких значениях a полином G(x) не является делителем F(x).
Запишите функцию. Например: f(x) = 3x2 + 6x -2. Эта квадратичная функция, и ее график – парабола Найдите вершину параболы. Если вам дана линейная функция или любая другая с переменной в нечетной степени, например, f(x) = 6x3+2x + 7, пропустите этот шаг. Но если вам дана квадратичная функция или любая другая с переменной х в четной степени, вы должны найти вершину графика этой функции. Для этого используйте формулу х=-b/2a.В функции 3x2 + 6x -2 a = 3, b = 6, c = -2. Вычисляем: х = -6/(2*3)= -1.[2]Теперь подставьте х= -1 в функцию, чтобы найти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 - 6 -2 = -5.Координаты вершины параболы (-1,-5). Нанесите ее на координатную плоскость. Точка лежит в третьем квадранте координатной плоскостиНайдите еще несколько точек на графике. Для этого подставьте в функцию несколько других значений х. Так как член x2 положительный, то парабола будет направлена вверх.[3]f(-2) = 3(-2)2 + 6(-2) -2 = -2. первая точка на параболе (-2, -2)f(0) = 3(0)2 + 6(0) -2 = -2. Вторая точка на параболе (0,-2)f(1) = 3(1)2 + 6(1) -2 = 7. Третья точка на параболе (1, 7).Найдите множество значений функции на графике. Найдите наименьшее значение у на графике. Эта вершина параболы, где у=-5. Так как парабола лежит выше вершины, то множество значений функции y ≥ -5.
Согласно теореме Безу остаток от деления полинома на двучлен равен значению полинома в корне этого двучлена,в данной задаче на полином G(x) никаких дополнительных условий не наложено,значит он может быть неприводимым над полем вещественных чисел,однако все равно раскладываться в произведение двучленов вида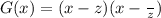
Где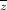 комплексно сопряжен z.
комплексно сопряжен z.
Полином G(x) примет вид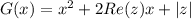
Re(z)-вещественная часть z,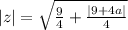 -модуль числа z.
-модуль числа z.
Очевидно,что подставляя получившиеся корни в исходный многочлен используя теорему Безу вычисление получается мягко говоря неудобным.
Аналогичная ситуация со схемой Горнера.
А вот при делении полиномов столбиком исходный многочлен представим в виде:
Очевидно,что степень остатка должна быть меньше степени делителя и мы можем остаток разделить на полином G(x),домноженный на (-a-3),тогда для того чтобы остаток от деления был равен нулю,то есть чтобы F(x) делился на G(x) должна выполняться система:
Которая не имеет решений ни в поле действительных,ни в поле комплексных чисел.
Значит ни при каких значениях a полином G(x) не является делителем F(x).