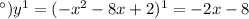
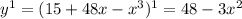
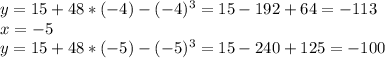

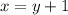
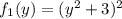 и
и 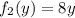
![(-\infty;0]](/tpl/images/0842/7775/15e33.png) и монотонно растет на промежутке
и монотонно растет на промежутке 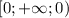
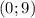
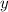 из промежутка
из промежутка ![(-\infty;0]](/tpl/images/0842/7775/15e33.png) выражение
выражение 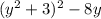 принимает положительные значения, так как вторая функция - монотонно растущая и при значении
принимает положительные значения, так как вторая функция - монотонно растущая и при значении 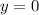 достигает лишь нуля, в то время, как вторая функция в принципе не принимает значений меньших за
достигает лишь нуля, в то время, как вторая функция в принципе не принимает значений меньших за 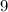 .
.![f_1'(y)=[(y^2+3)^2]'=2(y^2+3)(y^2+3)'=2(y^2+3)(2y)=4y^3+12y](/tpl/images/0842/7775/f5621.png)
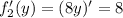
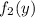 прибывает на 8
прибывает на 8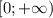 положительна, и уже при
положительна, и уже при 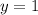 равна:
равна: 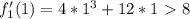 (и дльше только растет) т.е, первая функция после
(и дльше только растет) т.е, первая функция после 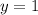 гарантированно растет быстрее чем вторая, при чем на момент
гарантированно растет быстрее чем вторая, при чем на момент 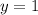 вторая функция не успела догнать первую:
вторая функция не успела догнать первую: 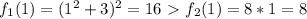
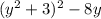 принимает исключительно положительные значения, и исходное неравенство действительных решений не имеет.
принимает исключительно положительные значения, и исходное неравенство действительных решений не имеет.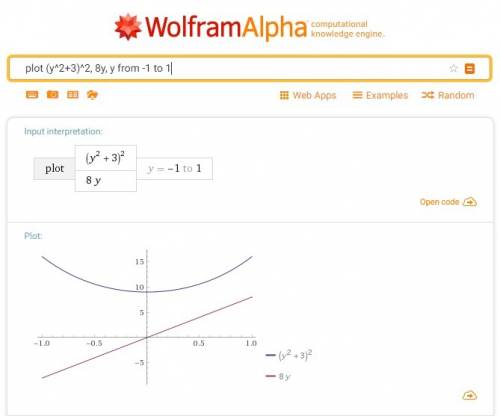
Возрастает при x>0, убывает при x<0. Наименьшее значение при x=0 y=-4.
Второй график - парабола ветвями вниз, смещённая на 1 вверх по оси OY.
Возрастает при x<0, убывает при x>0. Наибольшее значение при x=0 y=1