ответ: (2; 3)
Объяснение:
Решить графически уравнение:
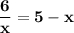
Построим два графика
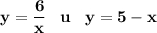
1.
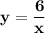
- функция обратной пропорциональности, график - гипербола.
Построим ветвь гиперболы:
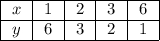
Вторую ветвь строим симметрично относительно начала координат.
2.
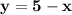
- линейная функция, график - прямая.
Для построения прямой достаточно двух точек:
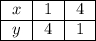
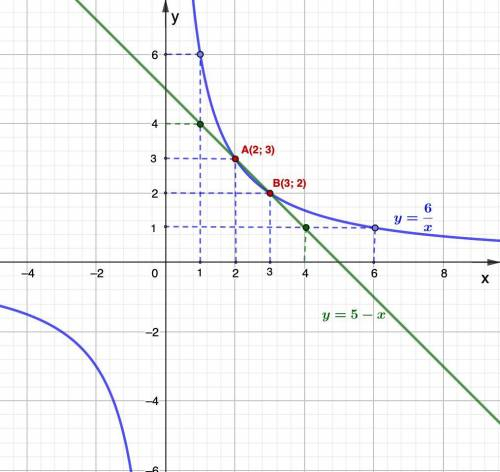
3. Построили графики.
Точки пересечения:
А (2; 3) и В (3; 2)
Решением уравнения будут абсциссы этих точек пересечения, то есть (2; 3).
В решении.
Объяснение:
Яка точка належить графіку рівняння x+y=9 (-6;-3); (6;3); (7;3); (1;9).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
а)x+y=9 (-6;-3);
-6-3= -9
-9≠9, не принадлежит.
б)x+y=9 (6;3);
6+3=9
9=9, принадлежит.
в)x+y=9 (7;3);
7+3=10
10≠9, не принадлежит.
г)x+y=9 (1;9)
1+9=10
10≠9, не принадлежит.
5=√25
√16<√17<√18<√19<√20<√21<и т.д<√25