y(x) = (x + x^2/2 + C)(1+x)^2
Объяснение:
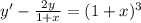
Это неоднородное уравнение, решается заменой:
y(x) = u(x)*v(x), тогда y'(x) = u'(x)*v(x) + u(x)*v'(x)
 (1)
(1)
Вынесем за скобки всё, что можно. У нас это только u:
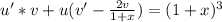 (2)
(2)
Скобку в левой части приравняем к 0:

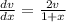

Получили уравнение с разделёнными переменными, интегрируем:
ln |v| = 2ln |1+x| = ln (1+x)^2
v(x) = (1+x)^2
Подставляем в уравнение (2):
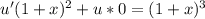
Делим всё уравнение на (1 + x)^2:
u' = 1 + x
Интегрируем:
u(x) = x + x^2/2 + C
Делаем обратную замену:
y(x) = u(x)*v(x) = (x + x^2/2 + C)(1+x)^2