Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
Объяснение:
4 < b < 7 (1)
подобные примеры решаются просто - домножаем все части неравенства, прибавляем/отнимаем от всех частей нужные числа, пока не получим посередине, то, что требуется в доказательстве
1) надо в средней части получить 13- 3b
умножим все части (1) на -3 (здесь помним, при умножении на отрицательное число знаки неравенства меняются на противоположные)
-12 > -3b > -21 (2)
добавим ко всем частям (2) +13
-12 + 13 > 13-3b > -21 +13 или -8 < 13-3b < 1 -что и требовалось доказать
2) здесь пойдем от обратного
если 1/m < 1/n, то это значит, что m < n
и тогда из нашего ответа
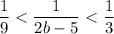
перепишем неравенство для знаменателей
получим
3 < 2b-5 < 9
теперь нам надо получить в середине b
прибавляем ко всем частям +5 и потом делим все части на 2
3+5 < 2b < 9+5
8 < 2b < 14
4 < b < 7 это и есть наша формула (1)
неравенство доказано.