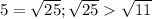
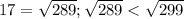
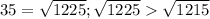
a) (x+2)+(x - 2)= x+2+x - 2=2х - раскрыли скобки, т.е. просто опустили и привели подобные.
б) (2x - 3y)*(2x +34)=4х²+68х-6ху-102у
в) (b² +4)*(4-b²)=(4+b² )*(4-b²)=4²-(b²)²=16-b⁴- при возведении степени в степень мы перемножаем показатели. как здесь 2*2=4.
г) (y+3)*(y-3)=у²-9
д) (3a-3y)*(2x+3y)=6ах+9ау-6ху-9у²
е) (b²+4)*(4-b²)=) (4+b²)*(4-b²)=16-b⁴
в номерах в), г), е) использовали формулу разности квадратов. т.е.
(а-с)*(а+с)=а²-с², в остальных б) , д), просто раскрывали скобки по распределительному закону, т.е. умножали все члены первой скобки на все члены второй
∫dx/(2x+1)=(2/2)∫dx/(2x+1)=∫2dx/(2*(2x+1))=∫d(2x)/(2*(2x+1))=
∫d(2x+1)/(2*(2x+1))=(1/2)∫d(2x+1)/(2x+1)=(1/2)㏑I2x+1I+c
есть такое понятие - инвариантность интеграла. т.е. формула справедлива для любого выражения из области определения.
Обратимся к таблице интегралов. есть формула ∫du/u=㏑IuI+c, я подогнал под эту формулу исходный интеграл. в качестве u у нас выступает (2х+1), здесь еще есть одна заковыка - дифференциал от 2х, он равен
d(2x)=(2x)'*dx=2dx- прочтите эту формулу справа налево, видите, что я заменил 2dx формулой d(2x)? у меня не было в условии двойки, формулу эту создал искусственно, т.е. умножил на два и разделил на два, ничего не случилось? иными словами умножил на единицу. но двойка в числителе, еще раз повторюсь, дала формулу d(2x), мы ее втянули под дифференциал, а двойка в знаменателе, так там и осталась до конца решения. Далее, чтобы использовать формулу ∫du/u=㏑IuI+c, надо, чтобы и под знаком дифференциала, и в знаменателе было одно и то же выражение. Поэтому втянули под дифференциал и единицу, получили, что 2*dx=d(2x)=d(2x+1), вопрос - а почему это можно делать? ответ прост - дифференциал функции - это производная функции (2x+1)'=2, умноженная на дифференциал аргумента dx, вот откуда эта формула взялась. Чтобы легко ориентироваться в данной теме, надо: знать таблицу интегралов, но на первом месте, разумеется, большое желание разобраться во всем этом самостоятельно.
2)∫dx/x²-налицо табличный интеграл, стоит только х² поднять в числитель, но уже с показателем -2, получаем ∫х⁻²dx=х⁻²⁺¹/(-2+1)+с=
х⁻¹/(-1)+с=(-1/х)+с
Резюме) здесь был использован табличный интеграл ∫uⁿdu=uⁿ⁺¹/(n+1)+c, и в качестве u выступала х⁻²
УДАЧИ.
5 > √11,т.к. у √11 нету чёткого корня,ближайший к нему корень √9(3) и √16(4),т.е. √11 примерно = 3,5.
17 < √299,т.к. у √299 нету чёткого корня,ближайший к нему корень - √289(17) и √324(18),т.е. √299 примерно = 17,5.
35 > √1215,т.к. у √1215 нету чёткого корня,ближайший к нему корень - √1156(34) и √1225(35),т.е. √1215 примерно = 34,8.