Объяснение:
+ - + - +
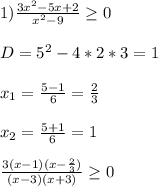
_____-3_________2/3______1___________3_______
x∈(-∞;3)∪[2/3; 1]∪(3; +∞)
+ - + - +
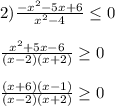
_______-6____________-2______1______2______
x∈(-∞; -6]∪(-2; 1]∪(2; +∞)
+ - + - +
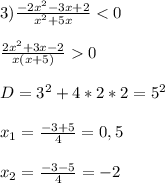
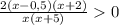
_____-5__________-2_____0____0,5______
x∈(-∞; -5)∪(-2; 0)∪(0,5; +∞)
+ - + - +
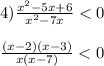
_______0_______2______3_________7________
x∈(0;2)∪(3;7)
(В конце знак "/" означает дробь, не деление)
Дана система уравнений:
2x-y=8
x-3y=8
Из первого уравнения выразим х:
2x-y=8
Переносим слагаемое из левой части в правую с заменой знака:
2x=8-(-y)
2x=y+8
Делим обе части уравнения на множитель:
= 
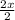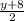
x =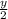 
+4
Подставляем найденное значение x во 2-ое уравнение:
x-3y=8
Получим:
-3y+(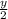+4)=8
4 - 
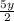=8
Переносим 4 (свободное слагаемое) из левой части в правую с заменой знака:
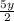-= - 4+8
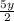-= 4
Теперь делим обе части на множитель, получается дробь (-1)5/2y /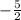 
= 4 /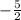
y =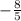 
И, т.к. x=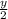+4, то x=
+4
Получается, что х =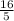 
ответ: x = 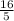, y = .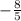
16^sin²x+16/(16^sin²x)-10=0
16^2sin²x-10*16^sin²x+16=0
16^sin²x=a
a²-10a+16=0
a1+a2=10 U a1*a2=16
a1=2⇒16^sin²x=2
2^4sin²x=2
4sin²x=1
sin²x=1/4
sinx=+-1/2
x=+-π/6+2πn,n∈z
a2=8⇒16^sin²x=8
2^4sin²x=2³
4sin²x=3
sin²x=3/4
sinx=+-√3/2
x=+-π/3+2πk,k∈z