y=11+6√x-2x√x D(f)=x∈(0:+∞)
2x√x=2*x¹*x¹/₂=2*x³/²
6√x=6*x¹/²
f(x)=-2*x³/²+6*x¹/²+11
(2*x³/²)`=3*x¹/²=3√x
(6*x¹/²)`=3/x¹/²=3/√x
(11)`=0
f`(x)=-3√x+3/√x
Приравниваем производную к нулю:
-3√x+3/√x=0
-3√x*√х+3=0
-3х+3=0
-3х=-3
х=1 - критическая точка.
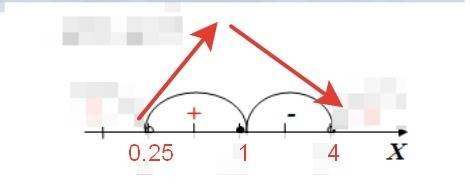
Чтобы узнать, достигает ли функция максимума в точке экстремума х=1, нужно определить знаки производной методом интервалов (рисунок во вложении):
f`(1)=0
f`(0.25)=-3√0.25+3/√0.25=4.5>0 - функция возрастает на отрезке (0;1)
f`(4)=-3√4+3/√4=-4.5<0 - функция убывает на отрезке (1;+∞)
При переходе через точку х=1 производная меняет знак с "+" на "-", значит х=1 - точка максимума функции.
Первый этап. Составление математической модели.
Пусть х сторона данного квадрата, сторона нового квадрата будет равна 5х. Площадь первого квадрата будет
S₁=x² см²
Площадь нового квадрата будет
S₂=(5x)²=25x² см²
По условию площадь нового квадрата на 384 см².
Получаем уравнение: 25х²-х²=384
Второй этап. Работа с математической моделью
25х²-х²=384
24х²=384
х²=384/24
х²=16
х=+-4 - по условию подходит только х=4
Третий этап. Получение ответа на вопрос задачи.
х - сторона исходного квадрата, х=4 см, значит сторона квадрата 4 см.
ответ 4 см сторона квадрата
поскольку F1 и F2 направлены в противоположные стороны
(направление как и у силы F1)
напарвление что у равнодействующей силы, т.е. в сторону F1