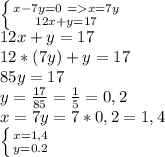
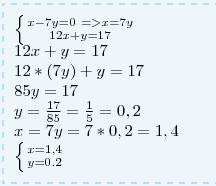
m=16,4 - при данном значении m прямые пересекаются в одной точке.
Объяснение:
Сначала выясним, точку пересечения двух первых прямых:
3х+1,2=2х+5
3х-2х=5-1,2
х=3,8 . Теперь надо найти ординату этой точки
у=2х+5
у=2*3,8+5
у=12,6.
Значит (3,8; 12,6) - точка пересечения двух первых прямых.
Так как все три прямые должны проходить через вышеуказанную точку, то третья точка тоже проходит через эту точку.
Теперь подставим эту точку в третью прямую
12,6=-3,8+m
m=12,6+3,8
m=16,4 - при данном значении m прямые пересекаются в одной точке.
Все слагаемые разделим на 6^x > 0;
3* 4^x / 6^x + 2*9^x / 6^x - 5* 6^x / 6^x < 0;
3 * (4/6)^x + 2* (9/6)^x - 5 *1 < 0;
3*(2/3)^x + 2 * (3/2)^x - 5 < 0;
(2/3)^x = t > 0; (3/2)^t = 1 / t ;
3 * t + 2 / t - 5 < 0; * t ≠ 0;
(3t^2 + 2 - 5t) / t < 0;
(3t^2 - 5 t + 2) / t < 0;
t > 0; ⇒ 3 t^2 - 5t + 2 < 0
t1 = 1; t 2 = 2/3;
3(t - 1)*(t - 2/3) <0;
используем метод интервалов
+ - +
(0)(2/3)(1) t
при t > 0; ⇒ t ∈ (2/3; 1);
составим двойное неравенство :
2/3 < (2/3)^x < 1;
(2/3)^1 < (2/3)^x < (2/3)^0;
2/3 < 1; ⇒ 0 < x < 1.
х∈ (0; 1)