Перенесем все влево и вынесем за скобки  :
:
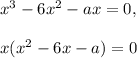
Из этого следует, что уравнение всегда имеет хотя бы одно решение -  . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения  и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении  корнем уравнения
корнем уравнения  будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 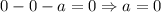 . При
. При  имеем:
имеем:

Делаем вывод, что при  уравнение имеет два корня:
уравнение имеет два корня: 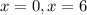 .
.
2) при 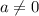 уравнение
уравнение  не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 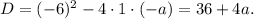
Здесь рассматриваем 3 случая:
2.1. Если  , то уравнение
, то уравнение  решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если 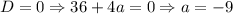 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 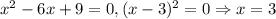 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если 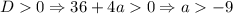 , то уравнение
, то уравнение  имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит  , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при  корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При  уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 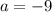 и
и  уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 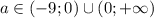 уравнение имеет три различных корня.
уравнение имеет три различных корня.
Решить системой? Хорошо. Вот вариант:
пусть X - скорость катера, тогда Y - скорость реки. Свяжем их уравнениями:
Поясню второе выражение: 2 часа это общее время движения, оно складывалось из времени движения
1) вниз (vniz) по течению
2) вверх (vniz) по течению
Решаем. Видно, что можно из первого высказывания взять 16 для второго высказывания. Получим:
Вспоминаем о нашей сисеме. После преобразований (см. выше) получили:
Вычитая или складывая почленно правые и левые части уравнений системы получим:
2X = 40
-2Y = -8, значит
Х = 20 км/ч, Y=4 км/ч
2,5z-z=-4,5+3
1,5z=-1,5
z=-1
б) 3x+5=0,5x+10
3x-0,5x=10-5
2,5x=5
x=2
в) 2,6+2x=1,9x+6,6
2x-1,9x=6,6-2,6
0,1x=4
x=4/0,1
x=40
г) x+x+1+x+2=9
3x=9-3
3x=6
x=2
д) z-2+z-1+z=-3
3z=-3+3
3z=0
z=0
e) 21+20-4x-11+2x=0
-2x=-30
x=15