17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
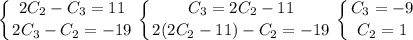
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,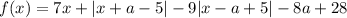 
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
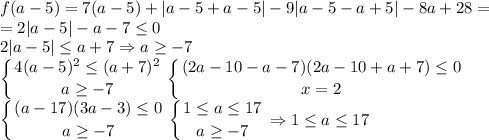
Наибольшее значение параметра — 17.
Постройте график функции у=х2-2х-8. Найдите с графика:
а) значение у при х=-1,5;
б) значение х, при которых у=3;
в) нули функции; промежутки, в которых у>0 и в которых у<0;
г) промежуток, в котором функция возрастает.
Для построения вычислим коорд. вершины: х0=-(-2)/2=1, у0=у(1)=1-2-8=-9
Нули ф-ции: у=0 х2-2х-8=0 х1=-2, х2=4
а) х=1,5 у≈ -8,75
б) х ≈ 4.5
в) Нули: х=-2; х=4
y>0 при х<-2 и х>4
y<0 при x€ (-2;4)
г) у возрастает при х>1 (1; +∞)
liliana
Администратор ( +3063 )
22.11.2014 21:50
Комментировать
№ 1. Построить график функции у=х2-2х-3, где х€(-∞;+ ∞) и определить область значения этой функции при указанных х.
График - парабола, ветви направлены вверх. Строится по схеме.
1) Находим нули функции, решая уравнение х2 -2х -3 = 0;
х1=-1; х2=3.
2) Координаты вершины параболы: х0=-b/(2a) = 2/2=1;
y0 = y(1) = 1-2-3 = -4
3) Найдем координаты точки пересечения графика с осью ОY:
x=0; y=-3.
4) Строим график по найденным точкам. Ось симметрии - прямая х=1
Можно вычислить значение функции в дополнительной точке, например, х=-2.
Получим у(-2) = 4+4-3= 5.
Область определения D(y)=R
Область значений Е(у)=[4; +∞).
Объяснение:
а) { y=x^2, x-y=-6;
из второго уравнения видно, что х=у-6
подставляем вместо "х" "у-6" в первое уравнение.
получаем квадратное уравнение с у-ом, решаем его, получаем корни: у=9;4, тогда
х=3;-2 (нашли из подстановки "у" в х=у-6)
б) { x+y=8, xy=12;
из первого уравнения видно, что х=8-у; подставим этот х во 2-ое уравнение, получим квадратное уравнение с "у". Решим его и получим, что корни у=6;2
найдем х, х=2;6
в) {x^2-Y^2=24, 2y-x=-7;
из 2-ого уравнения видно, что х=7+2у
подставим это во второе уравнение и получим квадратное уравнение с у, решив его, получим корни у=-1;-8(1/3).
найдем х, х=5;-9(2/3)
г) {x^2+y^2+3xy=-1, x+2y=0
из второго уравнения видно, что х=-2у, подстави это в 1-ое урав. и получим, что у^2=1; у=+-1.
тогда х=-2;2