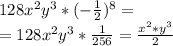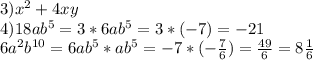Question

10 ! 1)представьте в виде многочлена стандартного вида выражение: (6х²-5х+²+х-7) 2) выражение: 128х²у³· ( -\frac{1}{2} )⁸ 3)вместо звездочки запишите такой многочлен,чтобы образовалось дождество: (4х²-2ху+у²*)=3х²+2ху 4)известно,что 6ab⁵=-7,найдите значение выражения 1.18ab⁵. 2.6a²b¹⁰ 7)докажите,что значение выражения (11n++11) кратно 7 при любом натуральном значении n

Answer 1

4)$128x^2y^3*(-\frac{1}{2})^8=\\=128x^2y^3*\frac{1}{256}=\frac{x^2*y^3}{2}$

$3)x^2+4xy\\ 4) 18ab^5=3*6ab^5=3*(-7)=-21\\ 6a^2b^{10}=6ab^5*ab^5=-7*(-\frac{7}{6})=\frac{49}{6}=8\frac{1}{6}$