![(1+tga)(1+tgb)=1+tga+tgb+tga\cdot tgb=\\\\=1+\frac{sina}{cosa}+\frac{sinb}{cosb}+\frac{sinasinb}{cosacosb}=\frac{cosa\cdot cosb+sina\cdot cosb+sinb\cdot cosa+sina\cdot sinb}{cosa\cdot cosb}=\\\\=\frac{(cosa\cdot cosb+sina\cdot sinb)+(sinacosb+sinbcosa)}{cosa\cdot cosb}=\\\\=\frac{cos(a-b)+sin(a+b)}{\frac{1}{2}(cos(a+b)+cos(a-b))}=[\, a+b=\frac{\pi}{4},\; b=\frac{\pi}{4}-a\, ]=\\\\=\frac{cos(a-\frac{\pi}{4}+a)+sin\frac{\pi}{4}}{\frac{1}{2}(cos\frac{\pi}{4}+cos(a-\frac{\pi}{4}+a))}=](/tpl/images/0325/7290/0c5b9.png)
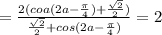
ответ ответ дан Solnishkosandra
№1.
а) 1. введу функцию у=3х^2 - 5х - 22.
2. Найду нули фунции через дискриминант:
D= 25 - 4 * 3 * (-22) = 25 + 264 = 289 , Д больше 0, 2 корня.
х1 = ( 5 - 17) / 6 = - 2; х2 = ( 5+ 17) / 6 = 3,7.
3. так как ветви параболы аправленны вверх, решение находится за корнями, то есть х принадлежит ( - бесконечность ; -2) ( 3, 7 ; + бесконечность)
в) 1. 2x^2 + 3х+ 8 = 0
2. D=9 - 4 * 2 * 8 = - 55. Д меньше 0, ветви параболы напр ввер, уравнение решения не имеет.
б) 1. х^2 = 81
х1 = 9, х2 = -9
2. так как ветви параболы направленны вверх, решение находится между корнями. то есть ответ: х принадлежит ( - 9; 9)
№2.
1.нули функции
х1=4, х2 = 1, х3= - 5
2. наносим значения на числовую прямую и
расставляем знаки
- + - +
(-5)(1)(4)> х
3. так как f(x) < 0 (по условию), то выбмраем интервалы, где знак (-), то есть ответ : х принадлежит ( - бесконечность; -5) , (1; 4)
№3
1. Введу ф-цию : 5x^2 + nx +20 = 0
2. D = n^2 - 4 * 5 * 20 = n^2 - 400.
3. Чтобы уравнение не имело корней, D должен быть меньше 0 ( так как при D<0 уравнение не имеет корней) Значит,
n^2 - 400 < 0
n^2 = 400
n1 = 20, n2 = - 20.
ответ: 20, - 20.