1) 6 км/ч; 2) 27 км/ч
Объяснение:
Пусть х - собственная скорость катера
х + 3 - скорость катера по течению реки
х - 3 - скорость катера против течения реки
По условию
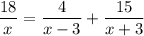
18(x² - 9) = 4x(x + 3) + 15x(x-3)
18x² - 162 = 4x² + 12x + 15x² - 45x
x² - 33x + 162 = 0
D = 33² - 4 · 162 = 441 = 21²
x₁ = 0.5 (33 -21) = 6 (км/ч)
х₂ = 0,5 (33 + 21) = 27 (км/ч)
По смыслу задачи и то и другое число подходит. Проверим.
1) 6 км/ч
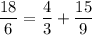
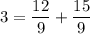
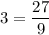
3 ≡ 3 (верно!)
2) 27 км/ч
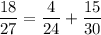
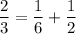
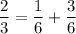
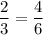
2/3 ≡ 2/3 (всё верно)
При движении с собственной скоростью 6км/ч путь займет у катера 3 часа, а при движении со скоростью 27 км/ч путь займёт 2/3 ч = 40 мин.
Дана функция y = (x^2 + 4)/(2x-3).
Её производная равна:
y' = (2x(2x-3) - 2(X^2+4))/((2x-3)^2) = (2x^2 - 6x - 8)/((2x - 3)^2).
Приравняем производную нулю (достаточно числитель).
2x^2 - 6x - 8 = 0 или, сократив на 2: x^2 - 3x - 4 = 0.
Д = 9 + 4*4 = 25, √Д = 5. х1 =(3 - 5)/2 = -1, х2 = (3 + 5)/2 = 4.
Первый корень нас не интересует, рассмотрим второй.
x = 3 4 5
y' = -0,889 0 0,245 .
Как видим, в точке х = 4 минимум функции (в том числе и на заданном промежутке). Значение функции в этой точке равно 4.
Определим значения функции на концах заданного интервала.
х = 2 8
у = 8 5,23.
ответ: наибольшее значение 8, наименьшее 4.
ответ: 2,5 кг