Последовательность является арифметической прогрессией тогда и только тогда, когда выполняется условие: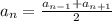 
. в нашем случае:
a(n)= 0,3x(n)+1
a(n-1)=0,3x(n-1)+1
a(n+1)=0,3x(n+1)+1
Докажем что у нас выполняется требуемое условие:
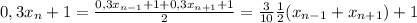
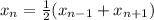
К этому свелось наше равенство. Если мы докажем, что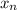 
арифметическая прогрессия, то мы докажем что 
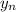арифметическая прогрессия.
Поскольку 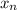у нас является натуральными числами от 1 до 10, то очевидно, что 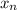арифметическая прогрессия. 
.
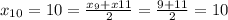Итак мы доказали, что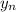 
арифметическая прогрессия. найдем ее сумму. По формуле: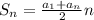 
Получаем:
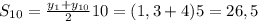
ответ: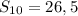 
3x+3x+2<90
6x<90-2
6x<88
x<14,6
2cos2x+5sinx-4=0
2(1-sin2x)+5sinx-4=0
2-2sin2x+5sinx-4=0
-2sin2x+5sinx-2=0 /(-1)
2sin2x-5sinx+2=0
Пусть sinx=t тогда 2t^2-5t+2=0
D = b2 - 4ac
D = 25 - 16 = 9 = 3^2
t1,2 = -b ± √D/2a
t1 = 5 + 3/4 = 8/4 = 2
t2 = 5 - 3/4 = 2/4 = 1/2
t1=2 t2=1/2
не подходить так как [1;-1]
sinx=1/2
ответ: x=(-1)pi/6+pin
Надо обе части каждого уравнения умножить (или разделить) на такое число, чтобы коэффициенты при одном из неизвестных были равны и имели разные знаки.
7x+5y=-5 Умножим на 35x+3y=1 Умножим на -5
Получаем 21х + 15у = -15
-25х -15у = -5
-4х = -20 х = -20 / -4 = 5.
у находим из любого уравнения: у = (1-5х) / 3 = (1-5*5) / 3 = -24 / 3 =
= - 8.