Для начала вспомним все три признака подобности треугольников:
I признак подобия треугольников - если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников - если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак подобия треугольников - если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Задача 1
∠ABC = ∠DEF = 90°, ∠ACB = ∠DFE = 55°, значит за первым признаком подобности треугольников ΔABC ~ ΔDEF.
Задача 2
Катеты - это прямые (в прямоугольном треугольнике), которые образуют прямой угол. Гипотенуза - это прямая, которая соединяет два катета. Значит, CV и VN - катеты, а CN - гипотенуза.
Задача 3
В прямоугольном ΔABC катеты AB и BC (AB = 5.9 см, BC = 5 см) образуют угол 90°.
В прямоугольном ΔDEF катеты DE и EF (DE = 5.9 см, EF = 5 см) образуют угол 90°.
Сделаем пропорцию:
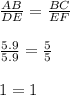
Значит эти треугольники подобные по второму признаку подобия треугольников
II признак подобия треугольников простыми словами - если одна сторона первого треугольника в k раз больше соответственной стороны второго, и вторая сторона первого треугольника тоже в k раз больше соответственной стороны второго, и эти две стороны в своих треугольниках создают углы, которые равны между собой, то эти треугольники подобны.
Если эти треугольники подобны, то все их углы равны между собой. Благодаря этому нам без разницы где находится меньшие углы: меньший угол ΔDEF будет находится там же, где и меньший угол ΔABC. Значит, меньший угол ΔDEF = меньшему углу ΔABC = 42°
1. Верно у предыдущего ответчика x+y=10
x*y=24
2. А вот со второй чего-то возможно такое:
Вся работа =100%
Т.о Бригада 2 выполняет 100% за x дней
1-ая бригада выполняет за x+10 дней
Теперь нужно понять сколько %-ов выполняет 2 бригада относительно первой (ниже назовем это а), т.е пропорция:
x 100%
x+10 неизвестно скока %( назовем это а)
т.е а*x=100(x+10)
a=(100*(x+10))/x
Теперь рассмотрим суммарную работу бригад т.к они работают вместе, то работа будет равна 200% т.о:
x+a=200%
x+(100*(x+10))/x)=200
100(x+10)+x^2=200x тут x^2-это x в квадрате
100x+1000+x^2=200x
x^2-100x+1000=0
Из квадратного уравнения получаем корни:
x1=50+Под корнем(-100/2)^2-1000
x2=50-Под корнем(-100/2)^2-1000
x1=50+под корнем (2500-1000)
x2=50-под корнем (2500-1000)
x1=11,3
x2=88,7дней
Это два варианта дней за которые может сделать работу вторая бригада, но т.к две бригады делают за 12 дней, значит ответ 11,3 не верный, ибо одна бригада делать должна дольше, чем если они работают совместно.
Т.к 1-ая бригада работает x+10:
x=88,7+10=98,7 дней
ответ: 1-ая 98,7 дней, 2-ая 88,7дней
А если просто система уровнений нужна, то просто напиши:
x+(100*(x+10))/x)=200
x+10=x2
x-это дни первой бригады, а x2- второй
3 задача.
S=210 км
S1=2/3S=210*2/3=420/3=140км путь до остановки
S2=210-140=70км- путь после остановки
Первая часть пути 140=t*V t-время потраченное на эти 140 км, V-это постоянная скорость с которой ехал поезд эти 140км
Вторая чать пути 70=(t/2-10/60)(V+10) t/2-это потому что на проезд пути ему нужно в 2 раза меньше времени, чем на преодоление первой части, т.к расстояние в 2 раза меньше 140км в 2 раза меньше 70км. -10/60 это те потерянные минутына остановке, при чем их нужно перевести в часы. поэтому 10 минут делим на 60. V+10 т.к скорость на втором участке увеличилась на 10 км/ч.
В итоге система уравнений:
140=t*V
70=(t/2-10/60)(V+10)
Выражаем из первого уравнения t=140/V и подставляем его во второе:
70=(140/2V-10/60)(V+10)
70=(70/V-1/6)(V+10)
70=(((420-V)/6V)*(V+10)
420V=(420-V)(V+10)
420V=420V-V^2+4200-10V V^2-это V в квадрате
V^2+10V-4200=0
Дальше ищем корни квадратного уравнения:
V1,2=-10/2+-корень из(10/2)^2+4200=-5+-65
V1=60км
V2=-70км т.к расстояние не может быть отрицательным, то ответ V=60км.
Чтобы решить подобное уравнение нужно извлечь корень.
Отв:
Чтобы решить такое уравнение нужно возвести обе части в степень корня и выполнить проверку.
Проверка:
ответ: