1) Первые 10 простых чисел, от 2 до 29:
2357111317192329
Чтобы получить наибольшее число, нужно вычеркнуть 235 и 111. Получится
7317192329
2) Пусть сумма всех чисел в каждой строке равна а.
Тогда сумма всех чисел в таблице равна М*а.
Сумма чисел в каждом столбце тоже равна а.
Тогда сумма чисел во всей таблице равна К*а.
Но это одно и тоже число.
М*а = К*а
М = К
ЧТД.
3) 1*2+2*3+3*4+4*5+5*6+6*7+7*8+8*9+9*10+...+997*998+998*999+999*1000
Выпишем последние цифры в каждом произведении.
2 + 6 + 2 + 0 + 0 + 2 + 6 + 2 + 0 + 0 +...+ 0 + 0 + 2 + 6 + 2 + 0 =
= (2+6+2) + 0 + (2+6+2) + 0 + ... + 0 + (2+6+2) + 0 = 10 + 0 + 10 + 0 +...+ 10 + 0
Эта сумма оканчивается на 0
4) Нельзя. Количество монет, лежащих орлом вверх, всегда четное.
Сначала 0, потом 20, потом 2 (если я переверну монету, которая осталась решкой вверх, и еще 19, которые стали орлом вверх), и так далее.
Оно не может стать нечетным числом 21.
5) Число 2017 нужно написать 9 раз подряд. Тогда каждая цифра будет повторена 9 раз, и сумма цифр будет делиться на 9, и само число тоже.
Количество цифр в этом числе 4*9 = 36.
6) Сегодня среда. Послезавтра будет пятница.
День, когда "послезавтра" станет "вчера" - это суббота.
День, когда "вчера" было "завтра" - это позавчера, в понедельник.
Понедельник и суббота одинаково далеки от воскресенья - на 1 день.
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4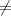 
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2
