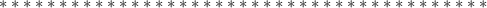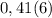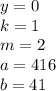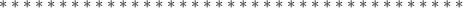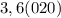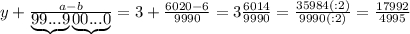![y= \frac{ \sqrt{6x+ x^{2} }+3 }{ \sqrt{x-3} } \\ \left \{ {{6x+ x^{2} \geq 0} \atop {x-30}} \right. =\left \{ {{x(6+x) \geq 0} \atop {x3}} \right. \\ x(6+x) \geq 0 \\ x_1=0; x_2=-6 \\ \\ \left \{ {{x \in (- \infty;-6] \cup [0;+\infty)} \atop {x3}} \right. = x \in (3;+\infty)](/tpl/images/0331/7237/4315a.png)

 ,
, , a
, a 
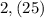
 целая часть. У нас она равна 2
целая часть. У нас она равна 2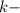 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25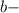 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.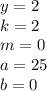
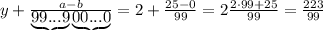
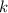 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 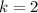 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 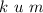 не стоит знак умножения
не стоит знак умножения