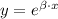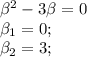
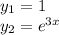
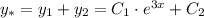
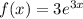
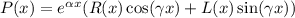.
, где R(x) и S(x) - полиномы, которое имеет частное решение.
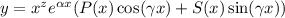, где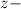 
кратность корня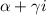 
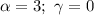
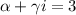является корнем характеристического уравнения кратности z=1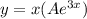
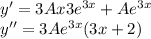
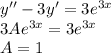
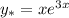
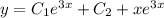
ответ: нет решения
Объяснение: Размещением из n элементов по х называется любое упорядоченное подмножество из х элементов множества, состоящего из n различных элементов. Число размещений без повторений определяется по формуле
Aₙˣ= n!/(n-x)! Значит A²ₙ= n!/(n-2)!
Eсли комбинации из n элементов по x отличаются только составом элементов, то такие неупорядоченные комбинации называют сочетаниями из n элементов по x. Число сочетаний без повторений из n элементов по x определяется по формуле:
Cₙˣ= n!/ x!(n-x)! значит Сₙ²= n!/ 2!(n-2)!
Поэтому Сₙ² : Аₙ²= n!/ 2!(n-2)! : n!/(n-2)! = 1/2! = 1/2, т.к. 2!= 1·2=2
1/2 ≠ 32, значит уравнение не имеет решения
Например: 5x – 4y + 6 = 0 .
Выразим y:
⇒ 4y = 5x + 6 ⇒ y = 5x+64 ⇒ y = 1,25x + 1,5 .
Полученное уравнение, равносильное первому, имеет вид
y = kx + m ,
где: x — независимая переменная (аргумент);
y — зависимая переменная (функция);
k и m — коэффициенты (параметры).