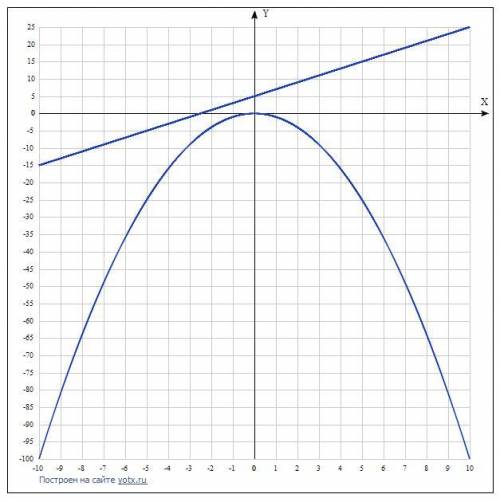
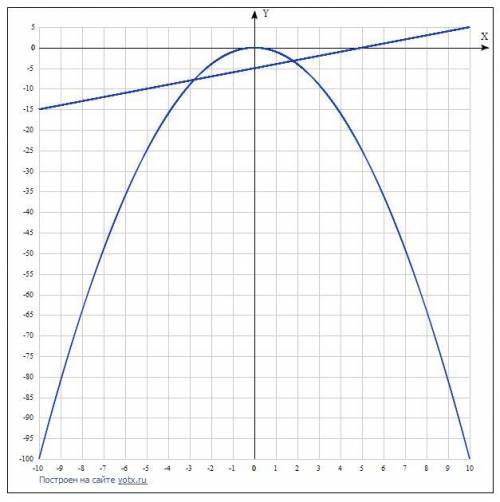
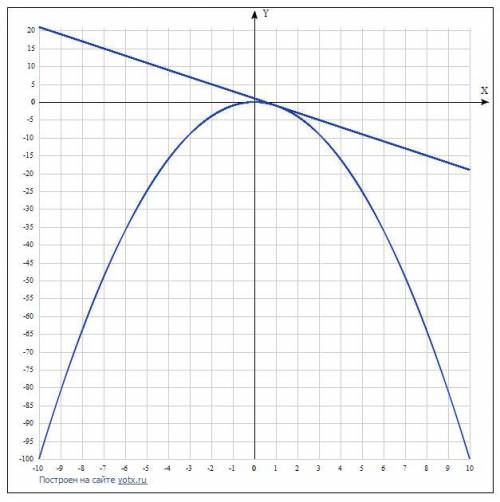
Функция: у=-х²
а) не пересекаются:
Тогда функция у=kx+m не должна проходить через точки, принадлежащие параболе у=-х². Например, это функция у=2х+5. Она не будет иметь с параболой общих точек (рис 1).
б) имеют две общие точки:
Тогда функция у=kx+m должна проходить через две точки, принадлежащие параболе у=-х². Например, это функция у=х-5. Она будет "пересекать" параболу (рис 2).
в) имеют одну общую точку:
Тогда функция у=kx+m должна проходить через одну точку, принадлежащую параболе у=-х². Например, это функция у=-2х+1. Она будет иметь с параболой только одну общую точку (рис 3). Или, как бы мы сказали в геометрии, она только коснётся параболы.
х₁= -√6 (≈ -2,5)
х₂=√6 (≈2,5)
Объяснение:
Координаты вершины параболы (0; -3), значит, х₀= 0, отсюда b=0; у₀= -3, отсюда с= -3.
Уравнение параболы у=ах²+bх+с.
Подставляем в уравнение известные значения х и у (координаты точки D(6; 15) и вычисляем а. Уже известно, что b=0, а с= -3:
15=а*6²+0*6-3
15=36а-3
-36а= -3-15
-36а= -18
а= -18/-36
а=0,5
Уравнение принимает вид: у=0,5х²-3
Решаем квадратное уравнение, находим корни, которые являются точками пересечения параболой оси Ох:
0,5х²-3=0
0,5х²=3
х²=6
х₁,₂= ±√6
х₁= -√6 (≈ -2,5)
х₂=√6 (≈2,5)
12/(х^2-2х+3)=х^2-2х-1
x^2-2x+1=t
12/(t+2)=t-2
12=t^2-4
t^2=16
t1=4
t2=-4
x^2-2x+1=4
x^2-2x-3=0
D=4+12=16=4^2
x1=(2+4)/2=3
x2=(2-4)/2=-1
x^2-2x+1=4
(x-1)^2=-4 Квадрат числа не может быть < 0
ответ: 3; -1