Question

1. найдите область определения функции: у = . 2. является ли четной или нечетной функция: g(x) = (x + 5)^3 - (x - 5)^3? 3. при каком значении b квадратный трехчлен 25 + 8b - b^2 принимает наибольшее значение? 4. изобразите схематически график функции: у = x^2 - 8|x| + 13. 5. найдите асимптоты графика функции у = . 6. постройте график функции у = |4 - x^2|. опишите свойства этой функции.

Answer 1

1. Подкоренное выражение неотрицательно, знаменатель не равен 0

$8-x \geq 0; 8 \geq x; x \leq 8;$

$x+5 \neq 0; x \neq -5$

обьединяя $D(y)=(-\infty;-5) \cup (-5;8]$

2. Область определения - множество всех действительных чисел, x є R

$g(-x) =(-x + 5)^3 - (-x - 5)^3=-(x-5)^3-(x+5)^3= -((x+5)^3-(x-5)^3)=-g(x)$

по определению функция g(x) нечетная

3.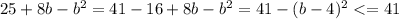 $25 + 8b - b^2=41-16+8b-b^2=41-(b-4)^2<=41$, причем равенство достигается при b=4

(так как квадрат любого выражения неотрицателен)

4. График во вложении

при x>=0 график имеет вид y=x^2-8x+13 вершина параболы (4;-3)

при x<0 график имеет вид y=x^2+8x+13 вершина параболы (-4;-3)

5. 2х-1=0

х=0.5 - вертикальная асимптота

ищем наклонные асимптоты

$k=lim_{x-\infty} \frac{y(x)}{x}=lim_{x-\infty} -\frac{6x-4}{(2x-1)x}=lim_{x-\infty} -\frac{6x-4}{2x^2-x}=0;$

$b=lim_{x-\infty} (y(x)-kx)=lim_{x-\infty} y(x)=lim_{x-\infty} -\frac{6x-4}{(2x-1)}=-\frac{6}{2}=-3$

значит наклонная будет одновременно горизонтальной асимптотой и равна y=-3

6. График во вложении

 Область определения D(y)=R

Область значений функций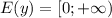 $E(y)=[0;+\infty)$

Функция четная, непериодичная

Функция положительная на R/{-2;2}

Нули функции х1=-2, х2=2

Функция убывает на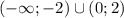 $(-\infty;-2) \cup (0;2)$

Функция возростает на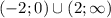 $(-2;0)\cup (2;\infty)$

х=-2 и х=2 - точки локального минимума (y(-2)=y(2)=0)

x=0 - точка локального максимума (y(0)=4)

Асимптот функция не имеет