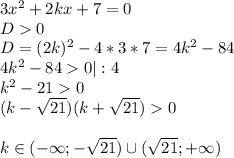
x=6
x³+3·x-234=(x-6)·(x²+6·x+39)
Объяснение:
Дан многочлен x³+3·x-234.
Корнем многочлена P(x) называется число с такое, что P(с)=0.
Поэтому решаем уравнение x³+3·x-234=0.
Из обобщённой теоремы Виета следует, что целые корни уравнения являются делителями свободного члена -234.
Рассмотрим делители числа:
1, 2, 3, 6, 9, 13, 18, 26, 39, 78, 117, 234.
Вычислением можно проверить, что только число 6 является корнем уравнения:
6³+3·6-234=216+18-234=234-234=0.
Тогда
x³+3·x-234=x³-216+3·x-18=x³-6³+3·(x-6)=(x-6)·(x²+6·x+6²)+3·(x-6)=
=(x-6)·(x²+6·x+36+3)=(x-6)·(x²+6·x+39).
Теперь рассмотрим уравнение
x²+6·x+39=0.
Так как D=6²-4·1·39=36-156= -120<0, то квадратное уравнение не имеет решений.
Тогда разложение многочлена имеет вид
x³+3·x-234=(x-6)·(x²+6·x+39).
x = 6; (x - 6)·(x² + 6x + 39)
Объяснение:
x³ + 3x - 234 = x³ + 3x - 18·13 = x³ + 3x - 18 - 18·12 = x³ - 27·8 + 3·(x - 6) = x³ - (3·2)³ + 3·(x - 6) = (x - 6)(x² + 6x + 36) + 3·(x - 6) = (x - 6)·(x² + 6x + 39);
x = 6 - корень многочлена; второй множитель - квадратный трехчлен с дискриминантом меньше 0, поэтому у него корней нет!
Примечание:
Для того, чтобы не догадываться до разложения многочлена на множители, можно воспользоваться свойством целых (ненулевых) корней целого алгебраического уравнения быть делителем свободного члена и поискать корень среди делителей числа 234:
±1; ±2; ±3; ±6 и т.д. Подойдет число 6. С схемы Горнера можно разделить x³ + 3x - 234 на x - 6:
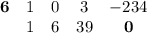
Получаем:
x³ + 3x - 234 = (x - 6)(x² + 6x + 39)