1
a)cos 260° * sin 190°
cos 260° < 0, (260° - угол 3 четверти, где косинус отрицателен)
sin 190° < 0(190° - угол 3 четверти, где синус отрицателен).
Поэтому это выражение больше 0.
б)cos 350° * tg(-100°)
cos 350° > 0(350° - угол 4 четверти, где косинус положителен).
tg(-100°) = -tg 100° > 0(100° - угол 2 четверти, где тангенс отрицателен, да ещё минус)
Поэтому, значение выражения больше 0.
2
а)sin 230° < 0, так как 230° - угол 3 четверти, где синус отрицателен.
б)cos 170° < 0, так как 170° - угол 2 четверти, где косинус отрицателен
в)tg 330° < 0, так как 330° - угол 4 четверти, где тангенс отрицателен
г)ctg(-220°) = -ctg 220° < 0, так как само выражение ctg 220° > 0(угол относится к 3 четверти, где котангенс положителен), да ещё минус прибавили.
д)В знаменателе у нас стоит постоянное число 8, так что знак выражения будет зависеть только от числителя. Достаточно проверить лишь одно из выражений, например, cos 3:
cos(3 * 57) = cos 171° < 0, (171 - угол 2 четверти, где косинус отрицателен). Поэтому всё выражение заведомом меньше нуля
Пусть двузначное число составлено из двух цифр a и b, причём a≠0 и b≠0. Тогда число можно представить в виде суммы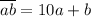 
.
Сразу проверим случай a=b : 
. Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.
Число кратно произведению цифр ab.
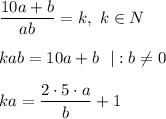
Так как числа ka и 1 - целые, значит, дробь должна тоже стать целым числом. Знаменатель b должен быть равен 1 или сократиться.
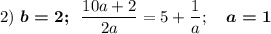
4) Число a или число 2a должны быть кратны цифре b. Возможные пары, помимо рассмотренных : (2;4), (3,6), (4,8), (6,3), (8,4), (9,3)
a = 2; b = 4; 
a = 3; b = 6;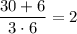 
Остальные варианты не подходят
a = 4; b = 8;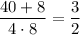 
a = 6; b = 3; 
a = 8; b = 4; 
a = 9; b = 3; 
ответ : 11, 12, 15, 24, 36
относительная 0,0005/3,142 примерно 0,016%