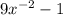
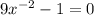
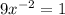
1.1.D(y)=[-5;4]
2.Е(у)=[-1;3]
3.Нули функции х=-3; х=3.5
4. Промежутки знакопостоянства. у>0 при х∈[-5;-3)∪(-3;3.5)
y<0 при х∈(3.5; 4]
5. Функция возрастает при х∈[-3;1] и убывает при х∈[-5;-3];[1;4]
6. Наибольшее значение у=3; наименьшее у=-1
7.Ни четная, ни нечетная.
8 Не периодическая.
2. f(10)=100-80=20
f(-2)=4+16=20
f(0)=0
5. 1.D(y)=(-∞;+∞)
2.Е(у)=(-∞;-1]
3.Нули функции нет
4. Промежутки знакопостоянства. у>0 ни при каких х, а при х∈(-∞;+∞)
y<0
5. Функция возрастает при х∈(-∞;-3] и убывает при х∈[-3;+∞)
6. Наибольшее значение у=-1; наименьшего нет
7.Ни четная, ни нечетная.
8 Не периодическая.
Находим первую производную функции:
y' = -1+9/(x^2)
или
y' = (-x^2+9)/(x^2)
Приравниваем ее к нулю:
-1+9/(x^2) = 0
x1 = -3
x2 = 3
Вычисляем значения функции на концах отрезка
f(-3) = 6
f(3) = - 6
f(1) = -10
f(4) = - 6, 25
ответ: fmin = -10, fmax = -6