3 насоса наполняют 2-й танкер за 40 часов.
Объяснение:
Исправим условие задачи.
"Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и ЧЕТВЕРТЬ второго, другого объема, за 11часов. Если бы три насоса наполнили первый танкер, а затем ТРЕТЬ второго, то работа заняла бы 18часов. За сколько часов три насоса могут наполнить второй танкер?"
Пусть х - время, за которое 1 насос наполняет танкер А
у - время за которое 1 насос наполняет танкер В.
По 1-му условию:
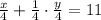
или
4х + у = 176 (1)
По 2-му условию:
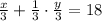
или
3х + у = 162 (2)
Вычтем из уравнения (1) уравнение (2)
х = 179 - 162
х = 14
Из уравнения (1) получим
у = 176 - 4х = 176 - 4 · 14 = 120
Один насос наполняет танкер В за 120 часов, тогда три насоса делают это в 3 раза быстрее, то есть за 40 часов
120ч : 3 = 40 ч
D=3²-4*1*(-10)=9+40=49>0
2 точки пересечения с Ох
Следовательно неравенства х²+3x-10<0 и x²+3x-10>0 имеют решения
y=x²+3x+10 - парабола, ветви вверх
D=3²-4*1*10=9-40=-31<0
нет точек пересечения с Ох
Следовательно вся парабола расположена выше оси Ох, значит
неравенство 4) x²+3x+10>0 имеет решения,
а неравенство 3) х²+3x+10<0 не имеет решений
ответ: 3) x²+3x+10<0 не имеет решений