Пусть первый может набрать весь текст за х часов, второй за y часов.
Примем всю работу за 1.
Значит, первый за час выполняет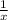 
часть работы.
Второй за час выполняет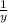 
часть работы.
Вместе за час они выполнят: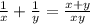 
За 8 часов выполнят: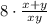 
, т.е всю работу 1
Первое уравнение:
Если первый оператор будет работать 3 ч,
а второй 12 ч, то они выполнят только 75%=0,75 всей работы.
Второе уравнение:
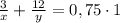
Решаем систему двух уравнений:
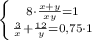
умножим первое уравнение на 3, второе уравнение на 4
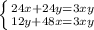
Приравниваем левые части:
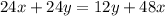
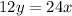
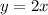
и подставляем в первое уравнение системы:
⇒ 
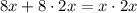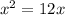( х=0 не удовл смыслу задачи)
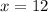
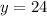
О т в е т. первый может набрать весь текст за 12 часов, второй за 24 часа.
f(x)=P(x)*g(x)
f(x) -четвертой степени g(x) - второй ,поєтому P(x) - второй степени
P(x)=cx^2+dx+e
4х^4-16x^3+3x^2+ax+b=(cx^2+dx+e)(x^2-4x+1)=
=cx^4+(-4c+d)x^3+(c+e-4d)x^2+(-4e+d)x+e
Методом неопределенніх коєффициентов ищем искомые параметры
x^4: c=4
x^3: -4c+d=-16
x^2: c+e-4d=3
x: -4e+d=a
1: e=b
c=4; d=-16+4c=-16+4*4=0
e=3+4d-c=3+4*0-4=-1
a=-4e+d=-4*(-1)+0=4
b=e=-1
ответ: при а=4 и в=-1