1.запишите верное неравенство которое получится, если: а) к обеим частям неравенства 8< 13 прибавить а) число 6.5; б) число -3.2б) из обеих частей неравенства 6> -5 вычесть а) число -5.4; б)число 9.3в) обе части неравенства 7> - 14 умножить а) на -4; б) на 1.5г)обе части неравенства -9< 12 разделить а) на 6; б) на -4
 км/мин.
км/мин.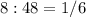 км/мин.
км/мин.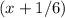 км/мин.
км/мин.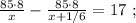
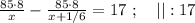
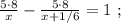
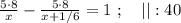
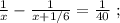
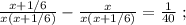
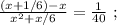
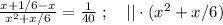
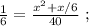
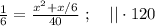
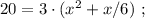
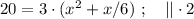
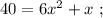
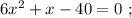
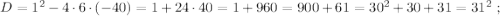
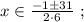
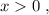 так, как это скорость,
так, как это скорость,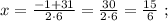
Умножаем на -1, при этом меняется знак неравенства
x(x - 7) < 0
По методу интервалов x ∈ (0; 7)
2) x^2*(3 - x)(x + 1) <= 0
Умножаем на -1, при этом меняется знак неравенства
x^2*(x - 3)(x + 1) >= 0
x^2 > 0 при любом x =/= 0. Поэтому x = 0 - это решение.
Делим на x^2
(x - 3)(x + 1) >= 0
По методу интервалов x ∈ (-oo; -1] U [3; +oo)
Добавим решение x=0 и получим:
x ∈ (-oo; -1] U [0] U [3; +oo)
3) 3x^2 - 7x + 2 < 0
D = 7^2 - 4*3*2 = 49 - 24 = 25 = 5^2
x1 = (7 - 5)/6 = 2/6 = 1/3; x2 = (7 + 5)/6 = 12/6 = 2
По методу интервалов x ∈ (1/3; 2)