По определению арифметической прогрессией является последовательность чисел в которой каждый последующий член начиная со второго получается прибавлением к предыдущему некоторого числа
пусть исходная последовательность
a, a+d, a+2d,
что если к каждому члену этой прогрессии прибавить одно и тоже число b, то получится последовательность
a+b, a+d+b, a+2d+b,
a+b, (a+b)+d, (a+b)+d,
получилась последовательность в которой первый член равен a+b а каждый последующий получается прибавлением d что по определению является арифметической прогрессией
Объяснение:
Объяснение:
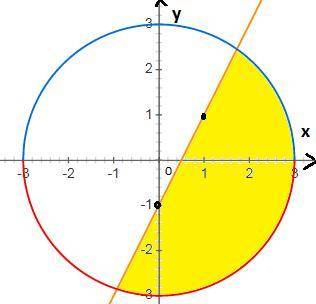
x²+y²≤9
x²+y²≤3²
это часть плоскости внутри окружности с радиусом R=3 и центром в начале координат и сама окружность
2х-у≥1
2х-1≥у
у≤2х-1 это часть плоскости ниже прямой у=2х-1
x²+y²≤9
x²+y²≤3² это часть плоскости внутри и на границе окружности и ниже прямой
Построим окружность с центром в начале координат и радиусом R=3
Построим прямую у=2х-1 по двум точкам
х=0 у=2х-1=2*0-1=-1 (0;-1)
х=1 у=2х-1=2*1-1=2-1=1 (1;1)
выделим цветом часть плоскости внутри и на границе окружности и ниже прямой
{х-1+ 2*√(х-1)(у+1) +у+1=9
{ху=5-х+у
{х+у+ 2*√ху+х-у-1 =9
{xy=5-x+y
подставляем второе в первое вместо ху:
x+y+ 2*√5-x+y+x-y-1 =9
x+y+ 2*√4 =9
x+y+4=9
x+y=5, x=5-y
подставляем в второе уравнение:
5y- y^2 =5-5+2y
y^2 - 3y=0
1) y=0 2)y=3
x=5 x=2