1.
Пусть:
x² = t
При этом t≥0
Тогда:
t² - 5t - 36 = 0
D = 25 + 36*4 = 169
t1 = (5+13)/2 = 9; t2 = (5-13)/2 = -4
t2 < 0 => корень уравнения один - t1.
x = √t, x = √9 = ±3
ответ: -3, 3
2. Дано:
s1 = 32 км
s2 = 12 км
t0 = 2 ч
u = 3 км/ч
Найти: v
А. Движение по течению:
v1 = v+u = v + 3, s1 = 32 км.
Б. Движение против течения:
v2 = v-u = v-3, s2 = 12 км.
В. t = s/v
2 = 32/(v+3) + 12/(v-3).
Откуда после несложных преобразований получаем:
v² - 22v + 21 = 0
v1 = 1, v2 = 21.
корень v1 не подходит, следовательно v = 21 км/ч
ответ: 21 км/ч
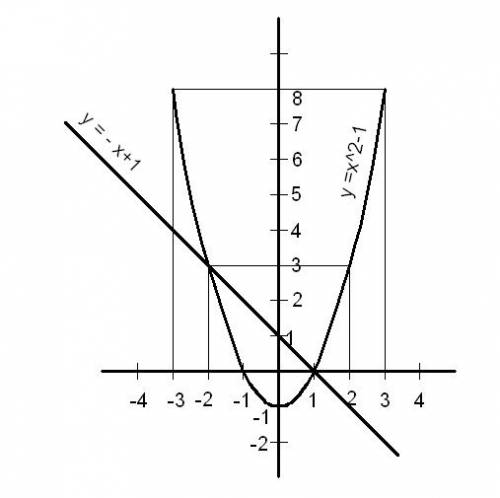
1) В точках пересечения координаты функцмй одинаковы надо приравнять их:
x^2 -1 =-x+1 x^2 + x -2 = 0 x = -1/2 =-V(1/4+2) = -1/2+-V(1/4 + 8/4) =-1/2 +-3/2
x1 =1 x2 = -2 Подставив эти значения, получим у1 = 0 у2 = 3.
2) координаты точек пересечения графика функции y=x^2-3x с осью x имеют значения у = 0.
x^2-3x = 0 х*(х -3) = 0 х1 = 0 х2 = 3.
3) координаты точек пересечения графика функции y=3x^2+5x-2 с осями координат: х =0
у = 0
При х = 0 у = -2
у = 0 3x^2+5x-2 = 0 x = -5 +-V(5^2 +4*3*2) / 2*3 = -5 +-V(25 + 24) / 6
x1 = 2/6 = 1/3 x2 =-2.