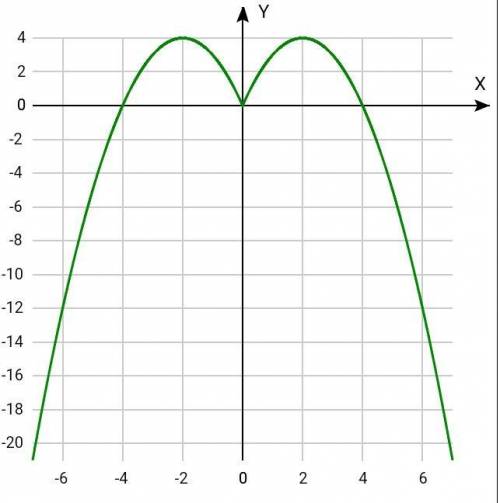
f(x) = 4|x| - x²
1. D(f) = R - симметрична относительно 0.
2. f(-x) = 4|-x| - (-x)² = 4|x| - x² = = f(x),
по определению f(x) - чётнвя.
График чётной функции симметричен относительно оси Оу.
3. Построим часть графика для х ≥ 0, а затем отобразим построенную часть симметрично относительно оси Оу.
f(x) = 4x - x² - квадратичная, графиком является парабола, ветви направлены вниз, т.к. а = - 1, а<0.
х вершины = - b/(2a) = -4/(-2) = 2;
у вершины = 4•2 - 2² = 4;
(2;4) - вершина параболы.
Найдём нули функции:
4x - x² = 0
- х (х - 4) = 0
х = 0 или х = 4
(0;0) и (4;0) - точки пересечения с осью Ох.
Изображение графика смотрите в прикреплённом чертеже.
б) (3х+3у)-(ах+ау)=3(х+у)-а(х+у)=(х+у)(3-а)
в) (ma-mb)+(a-b)=m(a-b)+(a-b)=(a-b)(m+1)