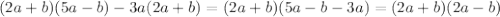
3) Противоположные боковые ребра образуют треугольник с диагональю основания, которая равна √2*√2=2= бок.ребру, значит, этот треугольник правильный, и любой угол в нем - 60°.
4) Рассмотрим диагональное сечение пирамиды. Так как высота вдвое меньше бокового ребра, угол при основании пирамиды будет равен 30° по теореме о гипотенузе, равной двум катетам. Все сечение - равнобедренный треугольник, значит, угол при вершине равен 180°-2*30°=120°.
5) Апофема (высота боковой грани) и боковое ребро дают прямоугольный треугольник с половиной ребра основания => половина ребра основания по теореме Пифагора = 1. Рассмотрим плоскость, в которой лежат апофема и высота пирамиды. Расстояние между основанием апофемы и основанием высоты равно половине ребра основания и равно 1. Значит, косинус угла между этой половиной и апофемой (а это и есть угол между боковой гранью и основанием) равен 1/2 (апофема равна 2), значит, угол равен 60°.
Раскрываем модуль по определению:
1-ax ≥0 ⇒ ax ≤ 1
Уравнение принимает вид:
1-ax=1+(1-2a)x+ax^2
ax^2+(1-a)x=0
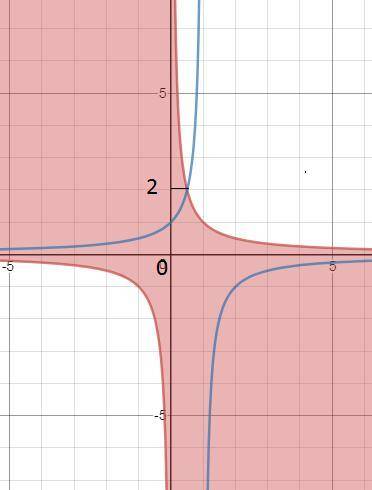
На плоскости хOа
ax ≤ 1 ⇒ a≤1/x- область между двумя ветвями гиперболы a=1/x
ax^2+(1-a)x=0 ⇒ ax^2+x-ax=0 ⇒ a·(x^2-x)=-x ⇒ a=-1/(x-1)
Уравнение имеет решение в области при
a∈(-∞;0)U(0;2]
см. рис.1
1-ax < 0 ⇒ ax > 1
Уравнение принимает вид:
-1+ax=1+(1-2a)x+ax^2
ax^2+(1-3a)x+2=0
На плоскости хOа
ax > 1 ⇒ a> 1/x- внешняя часть гиперболы a = 1/x
ax^2+(1-3a)x+2=0 ⇒ ax^2+x-3ax+2=0 ⇒ a·(x^2-3x)=-x-2 ⇒ a=-(х+2)/(x^2-3x)
Исследуем функцию с производной и строим график.
Уравнение имеет решение в области при
a∈(-∞;0)U [2;+∞)
см. рис. 2
ответ. a∈(0;2) U(2;+∞)