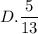
Объяснение:
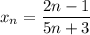
Если
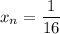 , то
, то
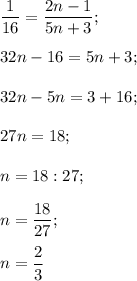
Так как полученное число n не является натуральным числом, то число 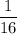 не является членом последовательности.
не является членом последовательности.
Если 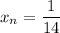 , то
, то
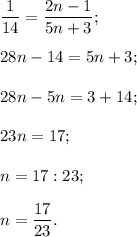
Так как полученное число n не является натуральным числом, то число
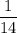 не является членом последовательности.
не является членом последовательности.
Если  , то
, то
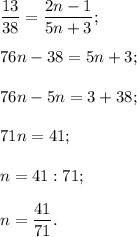
Так как полученное число n не является натуральным числом, то число
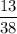 не является членом последовательности.
не является членом последовательности.
Если 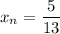 , то
, то
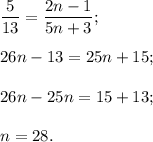
Так как полученное число n является натуральным числом, то число
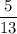 является 28 членом данной последовательности.
является 28 членом данной последовательности.
Если 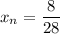 , то
, то
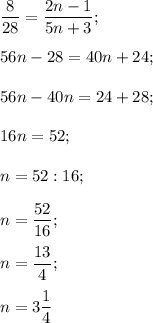
Так как полученное число n не является натуральным числом, то число
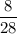 не является членом последовательности.
не является членом последовательности.
Тогда верный ответ: 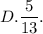
 ;
;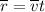 ;
;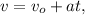 либо в векторном виде:
либо в векторном виде: 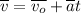 ;
;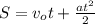 либо в векторном виде:
либо в векторном виде: 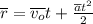 ;
;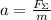 либо в векторном виде:
либо в векторном виде: 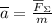 ;
; ;
;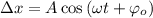 ;
;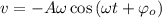 ;
; ;
;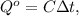 где
где 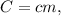 либо в удельном виде:
либо в удельном виде:  ;
;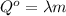 ;
;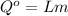 ;
; ;
; ;
;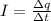 ;
;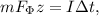 где
где  ;
;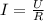 ;
;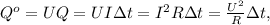
 ;
;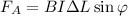 ;
; ;
;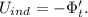
х - количество тетрадей/блокнотов в одной пачке
Составляем систему(оба уравнения в такой скобке { )
y(х+6)=120
ху = 90
Подставляем второе уравнение в первое и раскрываем скобки
90+6у=120
6у=30
у=5
Значит, было 5 пачек.
Что еще можно узнать:
В одной пачке тетрадок было 120/5 = 24 тетради(было пять пачек по 24 тетради)
В одной пачке блокнотов было 90/5 = 18 блокнотов(пять пачек по 18 блокнотов)