Объяснение:
Впервую очередь найдем стационарные точки. Для нахождения мы берем производную от исходной функции и приравниваем к нулю
f(x)=12sinx-6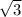
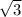x+π+6
f'(x)=12cosx-6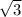
f'(x)=0
12cosx-6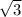=0
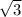cosx=/2
x=±π/6+2πk, k∈Z
итак подставляем в место k целые числа начиная с нуля для попадения в промежуток [0; π/2]
k=0;
x₁=π/6
x₂=-π/6 этот корень мы не берем так как не попадает в наш промежуток
k=1
x=π/6+2π=13π/6 уже не попадает в промежуток
значить мы нашли единственную стацианарную точку х теперь подставляем в наш начальную функцию и находим наибольшее значение.
х=π/6; fmax(π/6)=12*sin(π/6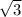)-6*π/6+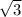π+6=12
Если ещё не изучено понятие производной, то решение может быть таким:
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
ОДЗ: 1) x - 2 > 0, x > 2
2) x > 0
ОДЗ: x ∈ (2 ; + ≈)
log₂ (x-2)* x = 3
x² - 2x = 2³
x² - 2x - 8 = 0
x₁ = - 2 не удовлетворяет ОДЗ
x₂ = 4
ответ: х = 4