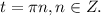 Если перебрать целые значения n, то получим числа:
Если перебрать целые значения n, то получим числа: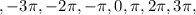 ....Это точки числовой окружности отмеченные, начиная с 0 через
....Это точки числовой окружности отмеченные, начиная с 0 через 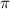 , (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и
, (т е через полкруга). против часовой стрелки положительные значения, по часовой - отрицательные. Положительные значения из промежутка [0;2π] мы можем показать на окружности, таких значений два: 0 и 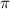 остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и
остальные будут совпадать с уже указанными, отрицательные значения из промежутка [-2π;0], их тоже два 0 и 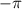 , для данной формулы тоже совпадут с уже указанными.
, для данной формулы тоже совпадут с уже указанными.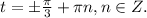 Это точки числовой окружности отмеченные, начиная с
Это точки числовой окружности отмеченные, начиная с 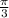 через
через 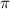 , (т е через полкруга) против часовой стрелки положительные значения, и начиная с
, (т е через полкруга) против часовой стрелки положительные значения, и начиная с  через
через 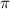 , (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения:
, (т е через полкруга) по часовой - отрицательные. И опять на промежутке [0;2π] мы можем показать на окружности только два значения: 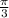 и
и 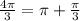 , остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:
, остальные совпадут с уже указанными, и на промежутке [-2π;0] тоже два значения:  и
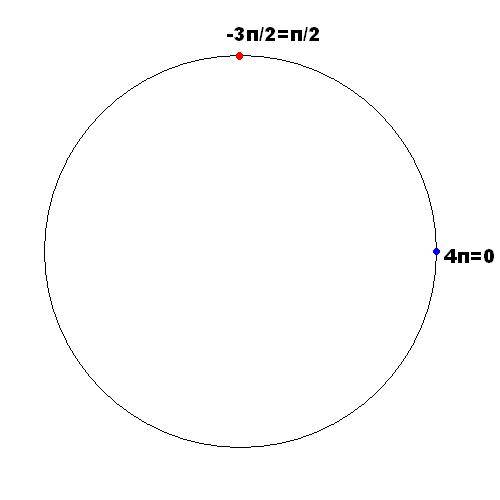
и 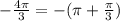 тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки:
тоже совпадут с уже указанными.В целом мы отметили на окружности 4 точки: 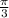 ,
, 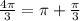 ,
,  ,
, 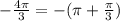 .
. 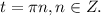 На промежутке [0;2π] два значения: 0 и
На промежутке [0;2π] два значения: 0 и 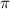 , остальные для
, остальные для 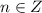 совпадут с уже указанными.
совпадут с уже указанными.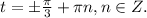 на промежутке [0;2π] два значения:
на промежутке [0;2π] два значения: 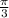 и
и 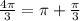 , на промежутке [-2π;0] тоже два значения:
, на промежутке [-2π;0] тоже два значения:  и
и 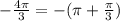 остальные для
остальные для 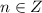 совпадут с уже указанными. Всего на окружности отмечено 4 точки:
совпадут с уже указанными. Всего на окружности отмечено 4 точки: 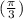 ,
, 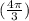 ,
, 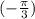 ,
, 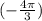 .
.
1. Диета: не больше 5-и тортиков в день:
2. Максимум может съесть 8 тортиков в день;
3. Условие, если 1 день - 8 тортиков,
то 2 следующих дня - по 3 тортика в день;
Если предположить, что с 01.12 до 31.12 сила воли слону не оказала ни разу, то слон съел бы за месяц (в декабре 31 день)
31*5=155 тортиков
Поскольку, по условию, сила воли иногда отказывает, то минимальное количество дней, когда слону отказала сила воли, = 1.
Если предположить, что слон съел максимальное количество тортиков, 8 шт, 31 декабря, то количество съеденного будет
30*5+8=158 тортиков, и диета - закончилась))
Если предположить, что день отказа силы воли пришелся не позже, чем 3 дня до конца декабря, то количество съеденных тортиков будет:
28*5+8+3+3=154 тортика
ответ: 158 тортиков
Сумму всех корней можно найти уже сейчас - ясно, что оба уравнения имеют по два корня, а значит, их сумму можно найти по теореме Виета. Сумма корней первого уравнения равна сумме корней второго уравнения и равна 1. Тогда сумма всех корней равна 2.
Для честности выпишем решения каждого из уравнений.
x^2 - x - 2 = 0: x1 = -1, x2 = 2
x^2 - x - 6 = 0: x3 = -2, x4 = 3