Выполните умножение 1) (3x^2-1)(2x^2+1) 2) (3x^2-1)(2x+1) ^2 это квадрат

Question

Алгебра: Выполните умножение 1) (3x^2-1)(2x^2+1) 2) (3x^2-1)(2x+1) ^2 это квадрат

alistas · Accepted Answer

Числа при делении на 9 могут давать остатки 0,1,2,3,4,5,6,7,8,9. поєтому любое натуральное число можно записать в виде

n=9m+r, где m - некоторое неотрицательное число, r - цифра

Используя формулу куба суммы

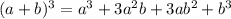
(a+b)^3=a^3+3a^2b+3ab^2+b^3

видим, что остаток от деления числа n^3 такой же как у числа b^3, так как

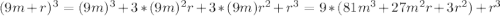
(9m+r)^3=(9m)^3+3*(9m)^2r+3*(9m)r^2+r^3=9*(81m^3+27m^2r+3r^2)+r^3

Рассмотрим остатки от деления кубов одноцифровых чисел

Кубы одноцифровых чисел 0, 1, 8, 27, 64, 125, 216, 343, 512, 729.

Числа 0, 27, 216, 729 при делении нацело на 9 дают остаток 0

Числа 1, 64, 343 при делении нацело на 9 дают в остатке 1

Числа 8, 125, 512 при делении нацело на 9 дают в остатке 8.

Таким образом делаем вывод, что кубы натуральных чисел при делении на 9 могут давать только остатка 0,1 и 8.

Доказано