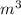 - 18
- 18 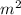 n + 18 m
n + 18 m 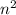 - 27
- 27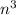
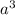 + 6
+ 6 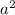 b + 6 a
b + 6 a 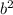 + 8
+ 8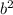
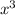 - 9
- 9 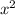 y + 9 x
y + 9 x 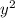 - 27
- 27
абсцисса вершины параболы: . тогда ординату вершины параболы найдем, подставив абсциссу вершины параболы в график уравнения
по условию, сумма координат вершины параболы равна 0,5. то есть
далее парабола пересекает ось ординат в точке с ординатой 0,25, то есть точка (0; 0.25) принадлежит параболе. подставим их координаты
отсюда абсцисса вершины параболы:
ответ: 0,5.