1. Найдите сумму бесконечно убывающей геометрической прогрессии 36: 12; 4; ...;
b1=36
b2=12
b3=4
q=b2/b1
s=b1/(1-q)
q=-12/36=-1/3
s=36/(1+1/3)=36/(4/3)=36*3/4=27
ответ: 27
2. Сумма бесконечно убывающей геометрической прогрессии равна 54. Найти, если
Если...? Тут как будто какого-то условия не хватает ((
3. Найдите сумму и первых членов арифметической прогрессии, если а=1, an=200, n=100
Sn = (a1 + an)/2* n
a1 = 1
an = 200
n = 100
S100 = (1 + 200)/2*100 = 201*50 = 10050
ответ: 10050
Объяснение:
Проверь второе задание, там будто реально условия не хватает.
1) 3
2) 1,5
3) 2/3
4) -0,9
5) 1
Объяснение:
1) 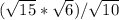 =
= 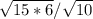 =
= 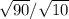 =
=  =
=  = 3
= 3
знак "/" - дробь; сначала я поставила числитель под один знак корня и перемножила числа, потом поставила все уравнение под знак корня, разделила 90 на 10 и получила 9. корень из 9 = 3
2) 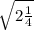 =
= 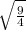 =
=  =
= 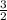 = 1.5
= 1.5
перевела дробь в неправильную (2 умножила на 4 и прибавила 1), получила 9/4. Поставила числитель и знаменатель отдельно под знак корня. Выразила из под корня 9 и 4. и получила 3/2.
3)  =
= 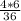 =
= 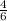 =
= 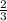
возвела скобку в степень. 2 поставила в квадрат. корень из 6 в квадрате равен подкоренному выражению (с любым числом под корнем получится число из под корня). получили 4 и 6. умножаем, сокращаем, получаем 4/6 или 2/3
4) 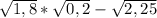 =
= 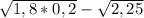 =
= 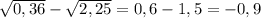
ставим 1,8 и 0,2 под один корень, перемножаем, получаем 0,36. выводим число из под корня. получаем 0,6 и 1,5, вычитаем, получаем -0,9
5) 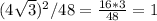
делаем то же самое, что и в 3 примере. 16 * 3 = 48
число, деленное само на себя ровно 1
x^2-1=(x-1)(x+1)