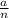Решить уравнение! (х+4)(х-3)+(х-5)(х+4)=0

Question

Алгебра: Решить уравнение! (х+4)(х-3)+(х-5)(х+4)=0

Artëm1646 · Accepted Answer

Решение: 1) Пусть у нас есть рациональное число, которое можно представить в виде дроби , где а - любое целое число, n - натуральное. По понятию множества действительных чисел, это любое число, которое есть в окружающем мире, будь то это -2, или 6,5. Но так, как  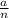- это рациональное число, а в виде рационального числа можно представить почти всякое число, то любое рациональное число является действительным. 2) Предположим, что выполняется и обратное утверждение, т.е. если число - действительное,...

MOGZ ответил