
Объяснение:
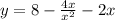
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
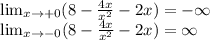
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
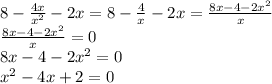
Решаем квадратное уравнение, находим точки пересечения с осью х:
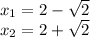
Находим точки экстремума (производная равна нулю).
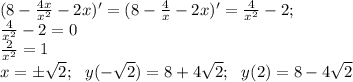
Для нахождения точек перегиба находим вторую производную
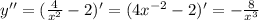
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
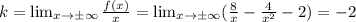
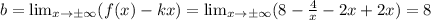
Наклонная асимптота есть:
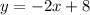
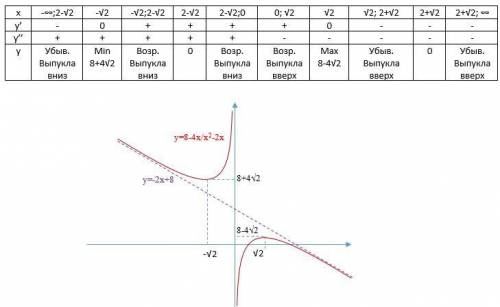
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
4
Запишем условие:
lgx + lg(x - 2) = lg(12 - x)
Складываем логарифмы в левой части, тогда:
lgx(x - 2) = lg(12 - x)
Так как 1 основание, решаем как обычное уравнение:
х(х - 2) = 12 - х
Раскороем скобки слева, откуда:
х^2 - 2х = 12 - х
Переносим правую часть влево, тогда:
х^2 - 2х - 12 + х = 0
Приводим подобные:
х^2 - х - 12 = 0
Решаем через дискриминант:
Находим дискриминант:
D = b^2 - 4ac
D = 1 - 4*1*(-12)
D = 1 - (-48)
D = 1 + 48 = 49
sqrt(D) = sqrt(49) = 7
x1 = (-b + sqrt(D))/2a = (1 + 7)/2 = 8/2 = 4
x2 = (-b - sqrt(D))/2a = (1 - 8)/2 = -3,5 - посторонний корень
Проверка:
Проверяем х1:
lg4 + lg(4 - 2) = lg(12 - 4)
lg4 + lg2 = lg8
Складываем логарифмы слева, тогда:
lg(4*2) = lg8
lg8 = lg8
Следовательно, х1 является действительным (правильным) корнем уравнения.
Проверяем х2:
lg(-3,5) + lg(-3,5 - 2) = lg(12 - 3,5)
lg(-3,5) + lg(-5,5) = lg8,5
Складываем логарифмы в левой части, тогда:
lg(19,25) > lg8,5
Следовательно, х2 посторонний корень данного уравнения.