Нехай за 
год перший робітник виконає завдання, а за 
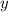год — другий. Тоді за одну годину перший робітник виконає 
усього завдання, а другий робітник — 
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто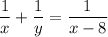 
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто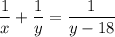 
Складаємо систему з двох рівнянь:
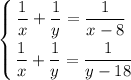
Тут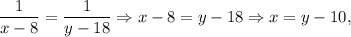 
оскільки ліві частини рівнянь рівні.
Підставимо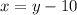 
в перше рівняння:
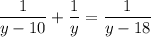
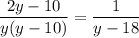
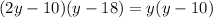
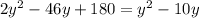
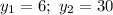
Якщ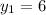о 
, то 
— не відповідає сенсу задачі.
Якщ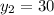о 
, то 
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.
Объяснение:
Пусть Х часов - время, которое необходимо первому рабочему для выполнения задания.
Тогда время выполнения вторым рабочим равно (Х + 4) часов.
2. Обозначим все задание за 1.
Тогда производительность первого рабочего 1/Х ед/час, второго - 1/(Х + 4) ед/час.
3. По условию задачи сначала первый рабочий работал 2 часа.
Тогда он выполнил 2 * 1/Х = 2/Х часть задания.
Затем второй рабочий работал 3 часа и выполнил 3 * 1/(Х + 4) = 3/(Х + 4) часть задания.
4. Вместе они сделали 1/2 часть работы.
2/Х + 3/(Х + 4) = 1/2.
4 * Х + 16 + 6 * Х = Х * (Х + 4).
Х * Х - 6 * Х - 16 = 0.
Дискриминант D = 6 * 6 + 4 * 16 = 100.
Х = (6 + 10) / 2 = 8 часов - время первого рабочего.
Х + 4 = 8 + 4 = 12 часов - второго.
ответ: За 8 часов может выполнить задание первый рабочий и за 12 часов - второй.
D=3²-4*2*(-5)=9+40=49>0; 2 корня
Х1=(-3+7)/4=4/4=1
Х2=(-3-7)/4=-10/4=-5/2=-2,5
2) х²-3х+5=0
D=(-3)²-4*5=9-20=-11<0; не имеет смысла, нет корней
3) 6х+1≥2х
6х+1-2х≤0
4х+1≤0
4х≥-1
х≥-1/4
(по поводу 3 не уверена)