36 см
Пошаговое объяснение:
Ширина =(42,8-2*12,4)/2=21,4-12,4=9
Периметр квадрата 9*4=36 см
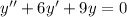
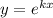 .
.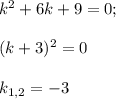
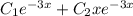
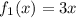 и
и 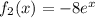
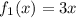
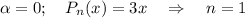
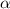 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.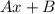
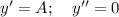 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 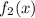 .
.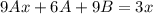
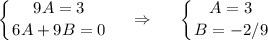
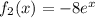
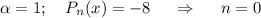
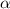 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: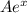
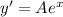 и
и 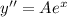
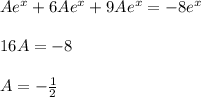
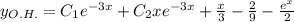
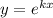 .
.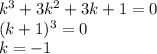
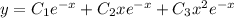
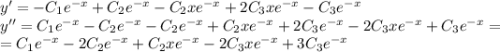
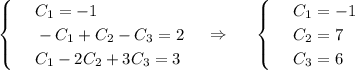
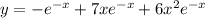
b-ширина a-длина
1дм 24мм=12,4см
P(прямоугольника)=2a+2b
42,8=2×12,4+2b
2b+24,8=42,8
2b=18
b=9
P(квадрата)=4×b=4×9=36