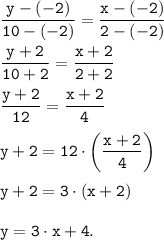1.1.D(y)=[-5;4]
2.Е(у)=[-1;3]
3.Нули функции х=-3; х=3.5
4. Промежутки знакопостоянства. у>0 при х∈[-5;-3)∪(-3;3.5)
y<0 при х∈(3.5; 4]
5. Функция возрастает при х∈[-3;1] и убывает при х∈[-5;-3];[1;4]
6. Наибольшее значение у=3; наименьшее у=-1
7.Ни четная, ни нечетная.
8 Не периодическая.
2. f(10)=100-80=20
f(-2)=4+16=20
f(0)=0
5. 1.D(y)=(-∞;+∞)
2.Е(у)=(-∞;-1]
3.Нули функции нет
4. Промежутки знакопостоянства. у>0 ни при каких х, а при х∈(-∞;+∞)
y<0
5. Функция возрастает при х∈(-∞;-3] и убывает при х∈[-3;+∞)
6. Наибольшее значение у=-1; наименьшего нет
7.Ни четная, ни нечетная.
8 Не периодическая.
y=3·x+4
Объяснение:
Абсцисса координат точек M(-2;-2) и N(2;10) различные (то есть прямая не проходит вертикально) и поэтому будем искать уравнение прямой в виде с угловым коэффициентом:
y=k·x+b.
Так как прямая проходить через точки M(-2;-2) и N(2;10), то подставим координаты точек в уравнение и получим систему уравнений относительно k и b:
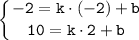
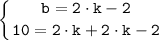
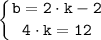
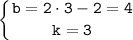
Подставляем найденные решения получим:
y=3·x+4.
Для решения задачи можно использовать общий вид уравнения прямой, проходящей через 2 точки M(x₁; y₁) и N(x₂; y₂):
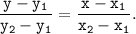
При заданных значениях координат M(-2;-2) и N(2;10) имеем: