2) x=0; x=-1,4;
4) m=0; m=0,75
6) u=0; u=2
Объяснение:
Общая идея, - вынесение множителя за скобки. Так и поступим:
2) 5x·x+7·x=0
Выносим общий множитель x: x·(5·x+7)=0
Результат умножения равен нулю, когда какой-либо из множителей равен нулю, следовательно:
x(1)=0 - первый корень;
5·x+7=0 тогда 5·x=-7 значит x=-7:5=-1,4
4) 4m·m-3·m=0
Выносим общий множитель m: m·(4·m-3)=0
Результат умножения равен нулю, когда какой-либо из множителей равен нулю, следовательно:
m(1)=0 - первый корень;
4·m-3=0 тогда 4·m=3 значит m=3:4=0,75
6) 3u·u+7=6·u+7
Наши "весы" в равновесии, снимем одинаковые "грузики", сохраняя равновесие весов:
3u·u+7=6·u+7 тогда 3u·u+7-7=6·u+7-7 значит 3u·u=6·u
Точно также мы имеем право ещё упростить выражение 3u·u=6·u, разделив обе части уравнения на 3:
3u·u=6·u
u·u=2·u
Отсюда видно, что u может принимать два значения: u(1)=0 и u(2)=2
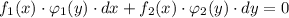
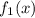и 
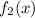зависят только от переменной "х" , а функци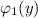и 
и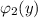 
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 
. 
.
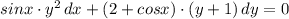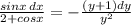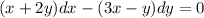, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 
.
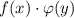(а-3)(а+4)-(а+2)(а+5)=(а²+4а-3а-12)-(а²+5а+2а+10)=а²+а-12-а²-7а-10= -6а-22
ответ -6а-22