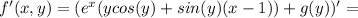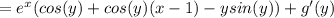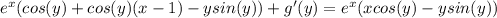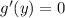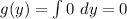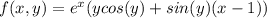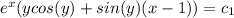Пусть f(x)=ax^2+bx+c. Данные уравнения могут быть записаны в виде
ax^2+(b-5)x+(c+20)=0;\ ax^2+(b-2)x+(c+8)=0.
По условию эти уравнения имеют единственные корни, что бывает тогда и только тогда, когда их дискриминанты равны нулю, то есть
(b-5)^2-4ac-80a=0;\ (b-2)^2-4ac-32a=0.
Домножим первое выражение на 2, а второе на 5, после чего возьмем их разность:
2(b-5)^2-8ac-5(b-2)^2+20ac=0;\ 12ac=3b^2-30;\ 4ac=b^2-10,
откуда дискриминант исходного квадратного трехчлена равен
b^2-4ac=b^2-b^2+10=10.
Таким образом, дискриминант равен 10, а значит наибольшее значение, которое он может принимать, также равен 10
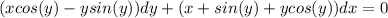
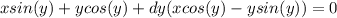
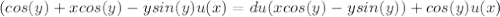
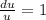
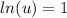
 ;
;