Дана система ур-ний 2x−y=19x−2 5y=14 Приведём систему ур-ний к каноническому виду −17x−y=−2 5y=14 Запишем систему линейных ур-ний в матричном виде [−17−1−20514] В 1 ом столбце [−170] делаем так, чтобы все элементы, кроме 1 го элемента равнялись нулю. - Для этого берём 1 ую строку [−17−1−2] , и будем вычитать ее из других строк: Во 2 ом столбце [−15] делаем так, чтобы все элементы, кроме 2 го элемента равнялись нулю. - Для этого берём 2 ую строку [0514] , и будем вычитать ее из других строк: Из 1 ой строки вычитаем: [−17−0−1−−1−2−−145]=[−17045] получаем [−170450514] Все почти готово - осталось только найти неизвестные, решая элементарные ур-ния: −17x1−45=0 5x2−14=0 Получаем ответ: x1=−485 x2=145
Объяснение:
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4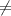 
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2
б) Если a > 0, то x < -a или x > a; если a = 0, то x ∈ R \ {0}; если a < 0, x ∈ R
в) Если a > 0, то -a < x < a; иначе решений нет.
г) Если a = 0, то x = 0; иначе x = +-a
д) |x - 1| + |x - 3| <= a
Если a < 0, корней нет (сумма двух модулей неотрицательна)
Если 0 <= a < 2, корней нет (геом. смысл модуля - расстояние до точки. |x - 1| + |x - 3| - это сумма расстояний до точек 1 и 3. Очевидно, эта сумма принимает своё наименьшее значение, равное двум, если x лежит между точками 1 и 3)
Если a = 2: 1 <= x <= 3 (см. предыдущее объяснение)
Пусть a > 2. Тогда (опять вспоминаем размышления о геом. смысле модуля) решение - все точки внутри отрезка [1, 3] + все точки, которые лежат вне отрезка, расстояние от которых до ближайшей из точек x = 1, x = 3 не превосходит (a - 2)/2. ответ на этот случай [1 - (a - 2)/2, 3 + (a - 2)/2]
ответ. Если a < 2, решений нет. Если a >= 2, x ∈ [2 - a/2, 2 + a/2]