Тангенс угла наклона касательной равен производной в точке касания к графику функции.
tgα = y'(x).
1) y = 0,2x^2 + 2x - 4, A(2; 0,8).
Проверяем - принадлежит ли точка данной функции.
0,2*2² + 2*2 - 4 = 0,8. Да, принадлежит.
Находим производную: y' = 0,2*2x + 2.
y'(2) = 0,2*2*2 + 2 = 2,8.
ответ: tgα = 2,8.
2) y = -3x^2 - x + 5, А(-2; -5).
Аналогично проверяем - точка А на кривой (парабола).
y' = -6x - 1,
y'(-2) = -6*(-2) - 1 = 12 - 1 = 11.
ответ: tgα = 11.
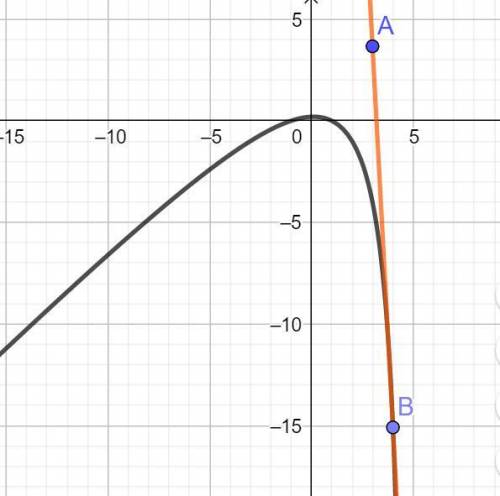
3) y = (x^2 - 1)/(x - 5), A(3; 3 2/3). (Ели так дано задание)
В этой задаче сложное решение, так как точка А не лежит на кривой.
Производная : y' = (2x(x - 5) - 1*(x^2 - 1))/(x - 5)^2) = (x^2 - 10x + 1)/((x - 5)^2).
Производная в точке касания хо: (xо^2 - 10xо + 1)/((xо- 5)^2).
Получим уравнение касательной проходящей через точку A(3;3 2/3):
3 2/3 = ((xо^2 - 10xо + 1)/((xо- 5)^2))(3 - хо) + ((xо^2 - 1)/(xо - 5)).
Решение затруднено, так функция - кубическая.
Ориентировочно решение найдено графически в программе ГеоГебра: у = -18,76х + 59,95.
График приведен во вложении.
Відповідь:
а)1+10/n , n={1 ; 2 ; 5 ; 10}
б (n-5)+6/n, n={1 ; 2 ; 3 ; 6}
Пояснення:
це дуже легко: ти маєш ш дріб під спільним знаменником, а тобі треба зробити зворотню дію:
а)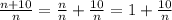 
( маєш суму , де 1- ціле , а 10/n- дробовий вираз)
від повідь на друге запитання : коли значення поданого виразу є цілим числом- тоді коли дробовий вираз 10/n буде цілим числом , тобто n буде дільником 10 і не більше 10 , тобто n має дорівнювати 1,2,5,10)
Коли дробовий вираз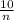 
буде цілим числом ,
n={1 ; 2 ; 5 ; 10}
б)тут та сама історія, просто є тричлен:
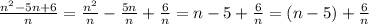
значення поданого виразу є цілим числом- тоді коли вираз 6/n буде цілим числом , тобто n має дорівнювати 1,2,3,6)
Коли дробовий вираз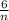 
буде цілим числом ,
n={1 ; 2 ; 3 ; 6}
5+7=12 сума,
5*7=35 добуток.