Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 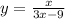 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)  при
при 
Если x = -5, то 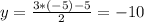
Если х= 3, то 
Значит, 
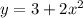
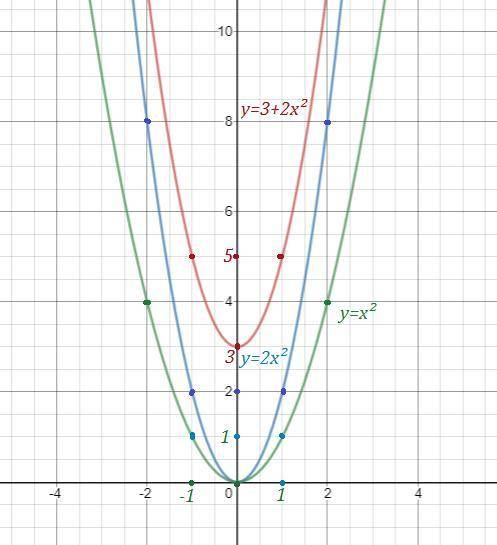
1) Строим параболу y=x² . Она прохy=3+2x² y=2x² y=x²одит через точки (0,0) - вершина , (-1, 1) , (1,1) .
2) Затем эту параболу растягиваем в 2 раза вдоль оси ординат (с коэффициентом k=2), и получаем параболу y=2x² . Она проходит через точки (0,0) - вершина , (-1,2) , (1,2) .
3) Теперь поднимаем параболу y=2x² на 3 единицы вверх вдоль рси ОУ, получаем параболу y=3+2x² . Её вершина в точке (0,3) . Проходит через точки (-1,5) , (1,5) .
4) Область определения заданной функции 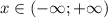 , а область значений
, а область значений 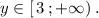
b) = sin^2x+cos^2x-cos^2x = sin^2x
c) = sin^2(3x)+cos^2(3x)-1 = 1-1 = 0